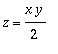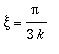Cinemática de la particula: Triedro de Frenet

J.Mª Goicolea, 8/10/2000

Una particula se mueve sobre el paraboloide hiperbólico 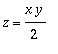, estando su posición definida por , .
Obtener los vectores del triedro intrínseco y el radio de curvatura, particularizando para .

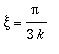> restart;

Definición de la trayectoria:

> x:=6*sin(k*xi);

> y:=-6*cos(k*xi);

> z:=1/2 * x*y;

Escribimos el vector posición:

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> vr:=vector([x,y,z]);

Calculamos su derivada respecto del parametro:

> vrp:=map(diff,vr,xi);

Definimos la función norma como raiz cuadrada del producto escalar de un vector por sí mismo

> norma:=proc(X)
sqrt(dotprod(X,X));
end:

Esta función sirve para calcular la derivada del arco respecto del parámetro :

> sp:=simplify(norma(vrp),symbolic);

El vector tangente se obtiene normalizando la derivada de la curva:

> vt:=evalm(1/sp * vrp);

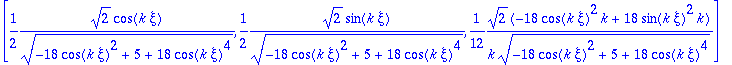
Particularizando en el punto pedido

> vt1:=subs(xi=Pi/(3*k),evalm(vt));

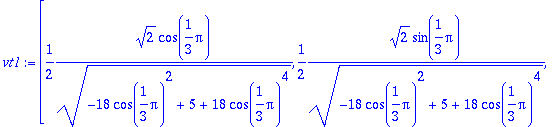
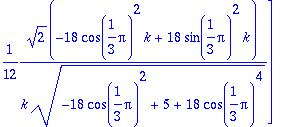
> vt1:=map(simplify,vt1);

> vt1f:=map(evalf,vt1);

Derivamos ahora de nuevo el vector tangente, respecto del parámetro :

> vtp:=map(diff,vt,xi);

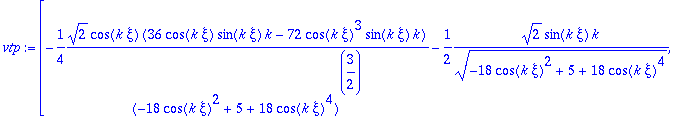
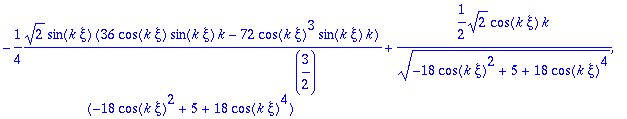
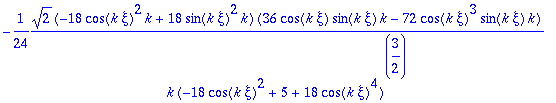
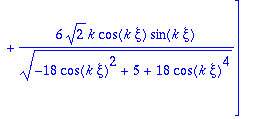
> vtp:=map(simplify,vtp,symbolic);

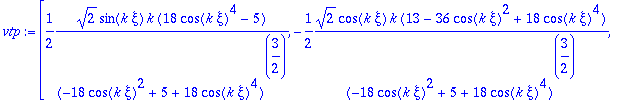
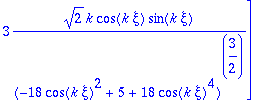
El vector normal principal se obtiene normalizando esta derivada:

> vtpn:=simplify(norma(vtp),symbolic);

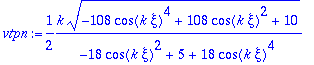
> vn:=evalm((1/vtpn)*vtp);

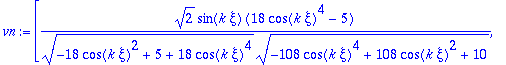
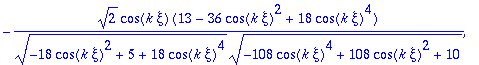
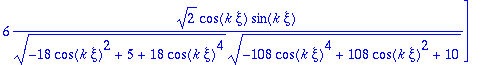
> vn:=map(simplify,vn,symbolic);

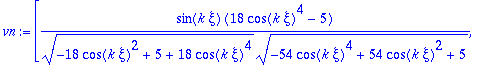
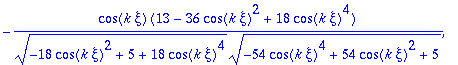
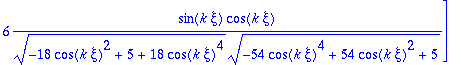
> vn1:=map2(subs,xi=Pi/(3*k),evalm(vn)):

> vn1:=map(simplify,vn1);

> vn1f:=map(evalf,vn1);

Calculamos ahora el radio de curvatura, en la posición pedida, como el inverso del m³dulo de la derivada del vector tangente respecto del arco . (Esta derivada se evalºa derivando primero la tangente respecto del parámetro .)

> R:=sp/vtpn;

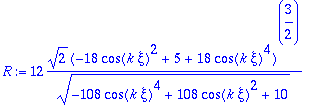
> R1:=simplify(eval(subs(xi=Pi/(3*k),R)));

> R1f:=evalf(R1);

Otra forma de calcular la curvatura es mediante la siguiente fórmula:

> vrpp:=map(diff,vrp,xi);

> kappa:=norma(crossprod(vrp,vrpp))/norma(vrp)^3;

> kappa:=simplify(kappa,symbolic);

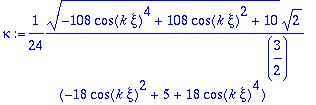
Por ultimo, obtenemos la binormal

> vb:=simplify(crossprod(vt,vn),symbolic);

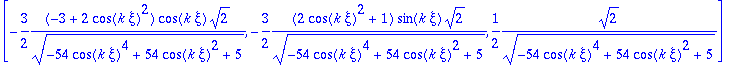
> vb1:=simplify(subs(xi=Pi/(3*k),evalm(vb)));

> vb1f:=map(evalf,vb1);

Dibujamos la curva junto con los vectores del triedro

> with(plots):with(plottools):

Warning, the name changecoords has been redefined

damos el valor unidad al parametro k

> c1:=subs(k=1,evalm(vr));

La función plots[spacecurve] crea el dibujo de la curva en 3D

> curva:=spacecurve(c1,xi=0..Pi,color=brown,thickness=3):

la función plottools[arrow] permite dibujar las flechas

> base:=subs(xi=Pi/3,evalm(c1)):

> tta:=arrow(base,evalm(3*vt1),[1,0,0],.3,.9,.1,color=green):

> nna:=arrow(base,evalm(3*vn1),[1,0,0],.3,.9,.1,color=red):

> bba:=arrow(base,evalm(3*vb1),[1,0,0],.3,.9,.1,color=black):

Dibujamos ahora todo el conjunto

> surf:=plot3d(u*v/2,u=0..6,v=-6..6):

> display(curva,tta,nna,bba,surf,view=-9..9,
axes=BOXED,scaling=CONSTRAINED,shading=Z,orientation=[30,75]);

Animación

> c2:=convert(c1,list);

> t2:=subs(k=1,convert(evalm(3*vt),list)):

> n2:=subs(k=1,convert(evalm(3*vn),list)):

> b2:=subs(k=1,convert(evalm(3*vb),list)):

> c3:=unapply(c2,xi);

> t3:=unapply(t2,xi):

> n3:=unapply(n2,xi):

> b3:=unapply(b2,xi):

> curva:=spacecurve(c2,xi=0..Pi,color=brown,thickness=3):

> surf:=plot3d(u*v/2,u=0..6,v=-6..6,style=contour):

> nump:=30:
dp:=Pi/nump:

> Q:=seq(display(curva,surf,view=-9..9,
arrow(c3(dp*n),evalf(t3(dp*n)),
[1,0,0],.3,.9,.1,color=green),
arrow(c3(dp*n),evalf(n3(dp*n)),
[1,0,0],.3,.9,.1,color=red),
arrow(c3(dp*n),evalf(b3(dp*n)),
[1,0,0],.3,.9,.1),color=black),
n=0..nump):

> display(Q,insequence=true,
axes=none,scaling=CONSTRAINED,shading=Z,orientation=[30,75]);