> restart:
Ejercicio 2, examen parcial 08/04/2000
José Mª Goicolea, Abril 2000
Un hexaedro regular, de masa
![]() y lado
y lado
![]() , cuyos vértices son OPQRSTUV está colgado de su v©rtice O a un punto fijo A mediante un hilo inextensible y sin masa. El cubo est¡ en reposo y una masa puntual
, cuyos vértices son OPQRSTUV está colgado de su v©rtice O a un punto fijo A mediante un hilo inextensible y sin masa. El cubo est¡ en reposo y una masa puntual
![]() impacta en el punto B del mismo, que es el centro de la cara OSVR, con velocidad horizontal y paralela al plano OSUQ, de módulo
impacta en el punto B del mismo, que es el centro de la cara OSVR, con velocidad horizontal y paralela al plano OSUQ, de módulo
![]() . Tras el impacto la partícula queda completamente adherida al punto B.
. Tras el impacto la partícula queda completamente adherida al punto B.
Se pide:
> with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
Masa del cubo
> masa:={m=rho*a^3};
![]()
Sean las direcciones (
![]() ) paralelas a las aristas. Momento de inercia de una rebanada perpendicular a
) paralelas a las aristas. Momento de inercia de una rebanada perpendicular a
![]() , respecto del eje
, respecto del eje
![]() , normal a la misma:
, normal a la misma:
> dI:=2*rho*int(int(v^2,v=-a/2..a/2),u=-a/2..a/2);
![]()
Momento de inercia del cubo, integrando:
> Iww:=int(dI,w=-a/2..a/2);
![]()
En función de la masa total del cubo
> inercia:={lambda=subs(solve(masa,rho),Iww)};
![]()
El eje
![]() es horizontal, segºn la dirección de la velocidad inicial de la partícula
es horizontal, segºn la dirección de la velocidad inicial de la partícula
![]() , el
, el
![]() vertical ascendente, y el
vertical ascendente, y el
![]() formando un triedro
formando un triedro
![]() a derechas. La expresión del vector velocidad de la partícula inicial es
a derechas. La expresión del vector velocidad de la partícula inicial es
> V0:=vector([v0,0,0]):
Las incógnitas del problema son los vectores velocidad de G y velocidad angular del cubo después del choque. Sabemos que la velocidad de G debe ser horizontal necesariamente, ya que el hilo impone esta misma condici³n a O, y el vector OG es vertical. Por tanto, establecemos la componente correspondiente igual a cero, eliminando una inc³gnita a priori:
> v[G]:=vector(3):v[G][3]:=0:evalm(v[G]);
> Omega:=vector(3):evalm(Omega);
![]()
![]()
Tensor de inercia esférico del cubo (en G):
> J[G]:=diag(lambda,lambda,lambda);
![J[G] := matrix([[lambda, 0, 0], [0, lambda, 0], [0,...](images/101exam19.gif)
Vector GB
> r[GB]:=(a/2)*vector([-1/sqrt(6),-1/sqrt(2),1/sqrt(3)]);
![]()
velocidad del punto B después de la impulsión (campo de velocidades del s³lido):
> v[B]:=v[G]+crossprod(Omega,r[GB]);
![]()
Impulsión reactiva del hilo, necesariamente vertical (y positiva o nula; si el resultado final fuese negativo, el hilo se arrugaría, y habrÂa que rehacer el cálculo poniendo
![]() ).
).
> Rv:=vector([0,0,R]):
Ecuación vectorial de balance de la cantidad de movimiento del conjunto cubo+partícula:
> eqv1:=evalm(m*V0+Rv)=evalm(m*v[B]+m*v[G]);
![]()
![]()
Las tres ecuaciones escalares a las que da lugar son:
> eq1x:=lhs(eqv1)[1]=rhs(eqv1)[1];
> eq1y:=lhs(eqv1)[2]=rhs(eqv1)[2];
> eq1z:=lhs(eqv1)[3]=rhs(eqv1)[3];
![]()
![]()
![]()
Ecuación vectorial de balance del momento cinético en G del cubo, considerando el momento de la percusi³n
![]()
> eqv2:=evalm(crossprod(r[GB],m*v[G]-Rv))=evalm(J[G]&*Omega);
![]()
Ecuaciones escalares correspondientes
> eq2x:=lhs(eqv2)[1]=rhs(eqv2)[1];
> eq2y:=lhs(eqv2)[2]=rhs(eqv2)[2];
> eq2z:=lhs(eqv2)[3]=rhs(eqv2)[3];
![]()
![]()
![]()
De estas ºltimas despejamos las componentes de
![]() , y las sustituimos en las anteriores ecuaciones:
, y las sustituimos en las anteriores ecuaciones:
> Omegas:=solve({eq2x,eq2y,eq2z},{Omega[1],Omega[2],Omega[3]});
![Omegas := {Omega[3] = 1/12*a*m*(-sqrt(6)*v[G][2]+3*...](images/101exam34.gif)
> eq1ax:=simplify(subs(Omegas,inercia,eq1x));
> eq1ay:=simplify(subs(Omegas,inercia,eq1y));
> eq1az:=simplify(subs(Omegas,inercia,eq1z));
![]()
![]()
![]()
Estas tres ecuaciones permiten despejar los valores de (
![]() ) que resuelven el problema:
) que resuelven el problema:
> solu:=simplify(solve({eq1ax,eq1ay,eq1az},{R,v[G][1],v[G][2]}));
![]()
Expresión de los vectores soluci³n:
> v[s][G]=simplify(subs(Omegas,inercia,solu,evalm(v[G])));
![]()
> v[s][B]=simplify(subs(Omegas,inercia,solu,evalm(v[B])));
![]()
> Omega[s]=simplify(subs(Omegas,inercia,solu,evalm(Omega)));
![]()
> R[s]=subs(inercia,solu,evalm(Rv));
![]()
> P[s]=subs(inercia,solu,evalm(m*v[G]-Rv));
![]()
Comprobación: balance cantidad de movimiento del conjunto
> compr1:=subs(solu,evalm(m*V0+Rv))=subs(Omegas,inercia,solu,evalm(m*v[B]+m*v[G]));
![compr1 := vector([m*v0, 0, 1/18*sqrt(2)*m*v0]) = ve...](images/101exam45.gif)
![compr1 := vector([m*v0, 0, 1/18*sqrt(2)*m*v0]) = ve...](images/101exam46.gif)
![]()
![compr1 := vector([m*v0, 0, 1/18*sqrt(2)*m*v0]) = ve...](images/101exam48.gif)
> simplify(compr1);
![]()
Comprobación: balance momento cinético del conjunto
> compr2:=crossprod(r[GB],m*V0)=subs(Omegas,inercia,solu,evalm(J[G]&*Omega+crossprod(r[GB],m*v[B])));
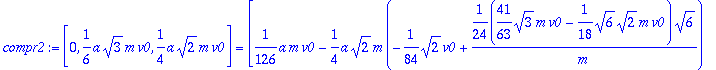
![]()
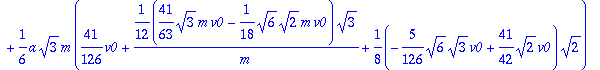
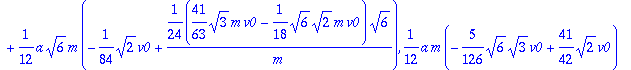
![]()
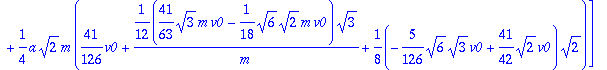
> simplify(compr2);
![]()