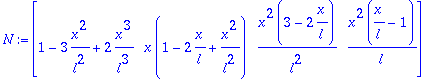
> restart:

> with(linalg):

Warning, new definition for norm

Warning, new definition for trace

Viga de Bernouilli-Euler

Jose Mª Goicolea Ruigomez,
10/02/2000

Funciones de forma cºbicas del elemento

> N:=matrix([[1-3*(x/l)^2+2*(x/l)^3,x*(1-2*x/l+(x/l)^2),
(x/l)^2*(3-2*x/l),x^2/l*(x/l-1)]]);

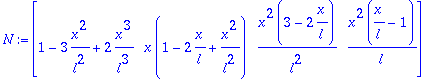
Vector de grados de libertad del elemento: flechas y derivadas de las mismas (=giros)

> a:=matrix([[w[1]],[wx[1]],[w[2]],[wx[2]]]);

Interpolación de flechas

> w[h](x):=multiply(N,a)[1,1];

Interpolación de curvaturas

> kappa[h](x):=diff(w[h](x),x,x);

Matriz de interpolación de deformaciones (curvaturas)

> B:=map(z->diff(z,x,x),N);

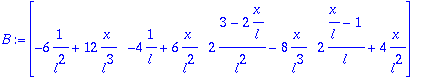
La curvatura (aproximada) es

> kappa[h](x):=multiply(B,a)[1,1];

Integrando de la matriz de rigidez del elemento

> Kb:=multiply(transpose(B),(E*J)*B);

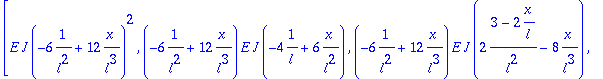
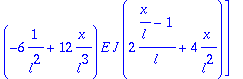
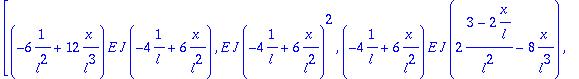
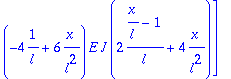
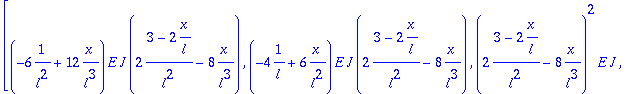
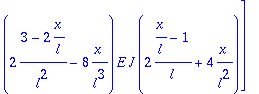
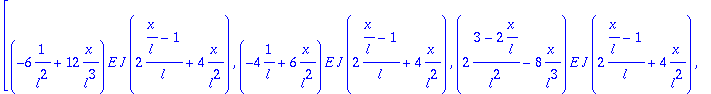
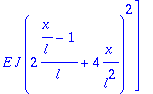
Integración para obtener la matriz de rigidez

> Kb:=map(z->int(z,x=0..l),Kb);

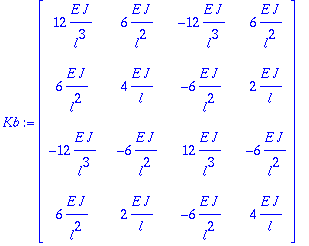
Viga de Timoshenko

Vector de grados de libertad: flechas y giros independientes

> a:=matrix([[w[1]],[theta[1]],[w[2]],[theta[2]]]);

Interpolacion de las flechas (lineal)

> Nx:=matrix([[1-x/l,0,x/l,0]]);

Interpolacion de los giros (lineal)

> Nt:=matrix([[0,1-x/l,0,x/l]]);

Flechas y giros interpolados

> w[h](x):=multiply(Nx,a)[1,1];

> theta[h](x):=multiply(Nt,a)[1,1];

Curvatura aproximada

>

Cortante aproximado

>

Funciones de interpolacion de deformaciones, para flexion y cortante

>

>

Las curvaturas y cortantes aproximados salen lo mismo que antes:

> kappa[h](x):=multiply(Bf,a)[1,1];

> alfa[h](x):=multiply(Bc,a)[1,1];

Matriz de rigidez por flexión

> Kf:=multiply(transpose(Bf),(E*J)*Bf);

> Kf:=map(z->int(z,x=0..l),Kf);

Matriz de rigidez por cortante

> Kc:=multiply(transpose(Bc),(G*A)*Bc);

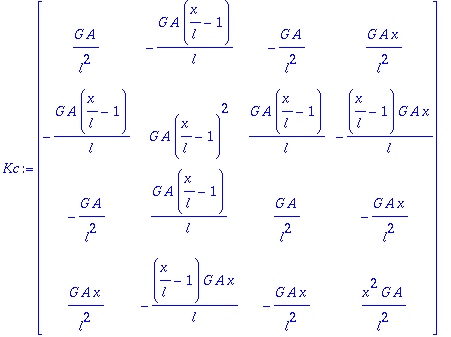
> Kc:=map(z->int(z,x=0..l),Kc );

Matriz de rigidez conjunta

> Kt:=evalm(Kf+Kc);

Ejemplo: ménsula empotrada en el extremo 1, con carga P en el extremo 2

Primero se resuelve con elementos viga de Timoshenko, con un sólo elemento.

El vector de cargas es

> carga:=matrix([[V[1]],[M[1]],[P],[0]]);

Lado izquierdo de la ecuación

> Kta:=multiply(Kt,a);

Las ecuaciones que interesan son las dos ºltimas (las primeras sirven para dar las reacciones)

> Kta[3,1]=carga[3,1];
Kta[4,1]=carga[4,1];

Sustituyendo las condiciones del empotramiento en 1

> tmp:=map(z->subs(w[1]=0,theta[1]=0,z),Kta);

Extraemos los coeficientes que dan la matriz de rigidez efectiva para los 2 g.d.l. del problema:

> Ke:=matrix([[coeff(Kta[3,1],w[2]),coeff(Kta[3,1],theta[2])],
[coeff(Kta[4,1],w[2]),coeff(Kta[4,1],theta[2])]]);

La inversa es la flexibilidad

> Fe:=inverse(Ke);

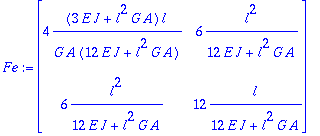
Veamos la expresión que resulta si se elimina el siguiente factor comºn de la matriz:

>

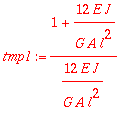
A falta del factor , la matriz de flexibilidad es:

> Fe1:=map(expand,map(simplify,evalm(tmp1*Fe)));

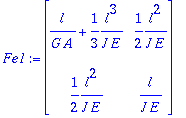
Calculemos ahora el valor exacto. Para ello, repetimos lo mismo pero con elementos viga de Bernouilli (exactos para flexión)

> Kba:=map(z->subs(w[1]=0,theta[1]=0,z),multiply(Kb,a));

> Ke:=matrix([[coeff(Kba[3,1],w[2]),coeff(Kba[3,1],theta[2])],
[coeff(Kba[4,1],w[2]),coeff(Kba[4,1],theta[2])]]);

> Feb:=inverse(Ke);

Añadimos la flecha por cortante y tenemos la flexibilidad de la solución exacta:

>

> evalm(Feb);

> evalm(Fe1)=evalm(Feb);

Vemos que se obtiene idéntico resultado que antes, pero en este caso no aparece el factor tmp1; .
Veamos el valor de este factor multiplicador, que indica la rigidización artificial de la ménsula, para un caso concreto con secci³n rectangular de ancho , canto y módulo de Poisson .

>

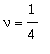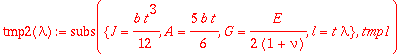
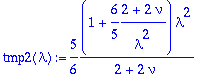
> tmp2(lambda):=simplify(subs(nu=1/4,tmp2(lambda)));

> plot(tmp2(lambda),lambda=1..50);

Viga de Timoshenko con integración reducida

Integrando de la rigidez a cortante

> Kc1:=multiply(transpose(Bc),(G*A)*Bc);

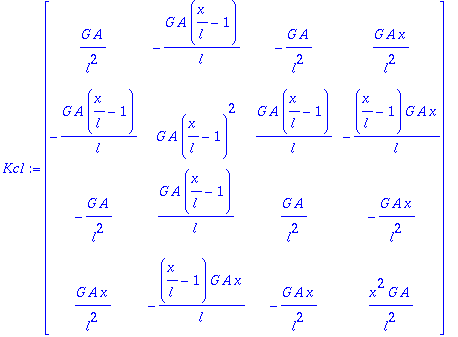
Particularizamos en el ºnico punto de integración que emplearemos, en el centro del elemento ( )

> Kc1:=map(z->subs(x=l/2,z),Kc1);

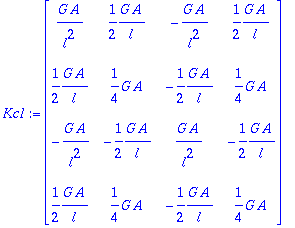
Integrando:

> Kc1:=map(z->int(z,x=0..l),Kc1);

Comparación entre la integraci³n completa ( ) y la reducida de 1 punto ( )

> evalm(Kc)=evalm(Kc1);

> Kt1:=Kf+Kc1;

Repetimos el ejemplo anterior de la ménsula:

> Kta:=multiply(Kt1,a);

Las ecuaciones que interesan son las dos ºltimas (las primeras sirven para dar las reacciones)

> Kta[3,1]=carga[3,1];
Kta[4,1]=carga[4,1];

Sustituyendo las condiciones del empotramiento en 1

> tmp:=map(z->subs(w[1]=0,theta[1]=0,z),Kta);

Extraemos los coeficientes que dan la matriz de rigidez efectiva para los 2 g.d.l. del problema:

> Ke:=matrix([[coeff(Kta[3,1],w[2]),coeff(Kta[3,1],theta[2])],
[coeff(Kta[4,1],w[2]),coeff(Kta[4,1],theta[2])]]);

La inversa es la flexibilidad

> Fe:=map(expand,inverse(Ke));

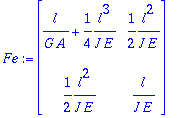
Comparación con la flexibilidad exacta: ya no aparece el término responsable del bloqueo, aunque la soluci³n difiere en el primer t©rmino (de a ). Esto origina un error que a medida que la discretización es más fina, se reduce. Si emple¡semos un s³lo elemento para la ménsula, en el límite de esbeltez infinita, la flecha calculada ser­a de la exacta. (Como hemos visto, esto es mucho más dram¡tico sin integración reducida: ¡la ménsula se bloquea y la flecha sale nula!)

> evalm(Feb)=evalm(Fe);

>