INTEGRAL DE CONVOLUCION

Doctorado: Analisis Sismico de Estructuras
Jose M. Goicolea, 12/03/2001

> restart:

Respuesta a una funcion impulso

> h:=t->1/(m*omega[d])*exp(-zeta*omega[0]*(t))*sin(omega[d]*(t));

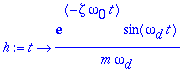
Integral de convolucion para una carga arbitraria

> Iconv:=int(p(tau)*h(t-tau),tau=0..t);

Sustituimos el valor de la frecuencia propia del sistema amortiguado

> Iconv:=subs(omega[d]=omega[0]*sqrt(1-zeta^2),Iconv);

Resultados para una carga de impacto (escalon), con y sin amortiguamiento.

> plot([1,
subs(p(tau)=1,zeta=0.00,m=1,omega[0]=1,Iconv),
subs(p(tau)=1,zeta=0.05,m=1,omega[0]=1,Iconv)],
t=0..6*Pi, color=[black,red,blue],thickness=3);

Expresion analitica para el caso sin amortiguamiento:

> simplify(subs(zeta=0,p(tau)=p[0],Iconv));

Probamos ahora con la funcion Heaviside (escalon) otra forma de hacer lo mismo:

> plot([Heaviside(t-2),
subs(p(tau)=Heaviside(tau-2),zeta=0.05,m=1,omega[0]=1,Iconv)],
t=0..6*Pi, color=[black,red],thickness=3);

Definimos una funcion rampa

> rampa := proc(x,T); min(x/T,1) end proc:

Integramos con una rampa cuya duracion sea exactamente igual a dos periodos del sistema sin amortiguamiento, para los casos sin amortiguamiento y con 5%. Se observa un curioso fenomeno en el caso sin amortiguamiento, al llegar a la meseta se "acopla" y la vibracion queda totalmente anulada

> plot([rampa(t,4*Pi),
subs(p(tau)=rampa(tau,4*Pi),zeta=0.00,m=1,omega[0]=1,Iconv),
subs(p(tau)=rampa(tau,4*Pi),zeta=0.05,m=1,omega[0]=1,Iconv)],
t=0..8*Pi, color=[black,red,blue],thickness=3);

Probamos ahora con otros periodos de la rampa, de 1.5 y 1 vez el periodo propio sin amortiguamiento:

> plot([rampa(t,3*Pi),
subs(p(tau)=rampa(tau,3*Pi),zeta=0.00,m=1,omega[0]=1,Iconv),
subs(p(tau)=rampa(tau,3*Pi),zeta=0.05,m=1,omega[0]=1,Iconv)],
t=0..8*Pi, color=[black,red,blue],thickness=3);

> plot([rampa(t,2*Pi),
subs(p(tau)=rampa(tau,2*Pi),zeta=0.00,m=1,omega[0]=1,Iconv),
subs(p(tau)=rampa(tau,2*Pi),zeta=0.05,m=1,omega[0]=1,Iconv)],
t=0..8*Pi, color=[black,red,blue],thickness=3);