
ESCUELA TéCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS (MADRID)
*[4mm]
 EXAMEN PARCIAL (9 de febrero de 1996)
EXAMEN PARCIAL (9 de febrero de 1996)
Ejercicio 2 Tiempo: 45min.

 {
{
0.4pt

}
Inicialmente la partícula sobre la mesa se halla a distancia b
del orificio, moviéndose con velocidad 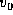 normal al hilo,
mientras que la otra está en reposo en la vertical del hilo.
Se pide:
normal al hilo,
mientras que la otra está en reposo en la vertical del hilo.
Se pide:
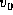 para que la masa inferior
permanezca inmóvil.
para que la masa inferior
permanezca inmóvil.
Llamaremos 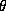 al ángulo girado por el hilo sobre la mesa, y T
a la tensión del mismo (T>0: tracción).
Escribimos en primer lugar las ecuaciones dinámicas para cada partícula:
al ángulo girado por el hilo sobre la mesa, y T
a la tensión del mismo (T>0: tracción).
Escribimos en primer lugar las ecuaciones dinámicas para cada partícula:
Eliminando T entre éstas:
Por otra parte, se conserva el momento cinético de la partícula superior respecto del orificio, al ser la tensión una fuerza central. Igualando al valor inicial del mismo,

Eliminando mediante esta expresión 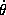 en la ecuación (2), resulta finalmente
en la ecuación (2), resulta finalmente
Eliminando  a partir de (3) en (1)
se obtiene
a partir de (3) en (1)
se obtiene

Inicialmente es  ; para que la partícula inferior permanezca
inmóvil debe ser
; para que la partícula inferior permanezca
inmóvil debe ser 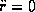 , con lo cual la superior describirá
una trayectoria circular alrededor del orificio con r=b. Entrando
con estos valores en (3) se obtiene
, con lo cual la superior describirá
una trayectoria circular alrededor del orificio con r=b. Entrando
con estos valores en (3) se obtiene

This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 639eyam.tex.
The translation was initiated by root on Fri Feb 16 21:06:03 GMT 1996