ENUNCIADO DEL EJEMPLO 6

    Un disco homogeneo de masa M y radio r gira por el perimetro de otro disco de masa M2 y radio dist estando ligado al eje del segundo disco por medio de una varilla de masa m y longitud l. Este segundo disco descansa horizontalemente sobre le plano XOY.

Se define entonces una ligadura anholonoma entre los dos discos.

   Paso 0. Reiniciación de las variables del sistema y llamada a los paquetes linalg, plots y plottools.

>

restart:

>	with(linalg):with(plots):with(plottools):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name changecoords has been redefined

Warning, the name arrow has been redefined

Además de estos paquetes básicos seránecesario cargar el paquete mecapac indicándole a Maple su situación exacta.

>	libname:="C:/",libname;

>	with(mecapac3d):

   Paso 1. Definimos las coordenadas generalizadas theta y phi del sistema en una lista que se denominará cg.

>	cg:=[theta,phi]:

   Paso 2. Definición mediante variables de los elementos que forman el sistema mecánico. Es decir, la varilla y los dos discos.

>	rot1:=rota(theta,3):

>	rot2:=rota(-Pi/3,2):

>	rottot:=evalm(rot1&*rot2):

Definimos las coordenadas del centro de masa de la varilla.

>	xg:=[l/2*sin(Pi/3)*cos(theta),l/2*sin(Pi/3)*sin(theta),r*sin(Pi/3)+l/2*cos(Pi/3)];

Definimos la varilla.

>	v1:=[varilla,xg,rottot,m,l];

Ahora hacemos exactamente lo mismo con los dos discos.

>	rotpd:=rota(theta,3):

>	rot3:=rota(-Pi/3,2):

>	rot4:=rota(phi,3):

>	r2:=evalm(rot3&*rot4):

>	rottot2:=evalm(rotpd&*r2):

>	xg2:=[l*sin(Pi/3)*cos(theta),l*sin(Pi/3)*sin(theta),r*cos(Pi/6)]:

>	d1:=[disco,xg2,rottot2,M,r];

Definimos ahora el segundo disco

>	dist:=l*sin(Pi/3)-r*sin(Pi/6):

>	rot5:=rota(0,1):

>	d2:=[disco,[0,0,0],rot5,M2,dist];

   Paso 3. Definición de los elementos gráficos que definiran nuestro sistema de ejes.

>	a2:=[angulo,[(dist/2),0,0],[0,0,0],[(l/2*sin(Pi/3)*cos(theta))/2,(l/2*sin(Pi/3)*sin(theta))/2,0],(dist/2)]:

>	ejeX:=[vector,[0,0,0],[10,0,0],red]:

>	ejeY:=[vector,[0,0,0],[0,10,0],green]:

>	ejeZ:=[vector,[0,0,0],[0,0,10],blue]:

>	TO := [texto,[0,0,-1],"O"]:

>	TX := [texto,[10,0,-1],"X"]:

>	TY := [texto,[0,10,-1],"X"]:

>	TZ := [texto,[0,0,11],"Z"]:

   Paso 4. Definición de la variable sistema que agrupa en una lista todos los elementos anteriores.

>	sistema:=[v1,d1,d2,a2,ejeX,ejeZ,ejeY,TO,TX,TY,TZ];

   Paso 5. Obtención de la energía potencial del sistema mediante fV asignándola a la variable V.

>	V:=fV(sistema);

   Paso 6. Obtención de la energía cinética del sistema mediante fT asignándola a la variable T.

>	T:=simplify(fT(sistema));

   Paso 7. Obtención de la lagrangiana como diferencia de energías entre la energía cinética y la potencial.

>	L:=simplify(T-V);

   Paso 8. Puesto que las ligaduras son anholonomas definimos la ligadura mediante la relacion de velocidades en el centro instantaneo de rotacion del disco que gira.

>	Phi:=[theta1*dist-phi1*r];

Hallando la reaccion producida en ese punto

>	reacc:=Fc();

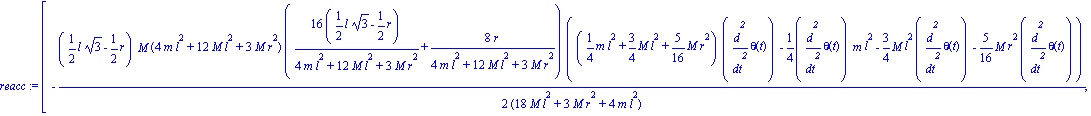
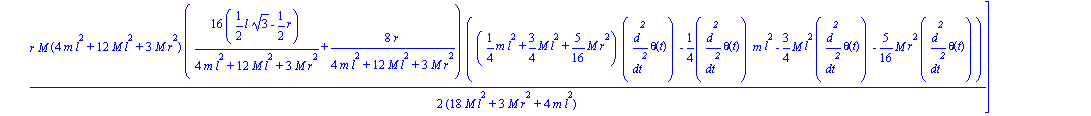
Particularizamos en el instante t=1.Quedando solo en funcion de las dimensiones del sistema.

>

reacc[1];

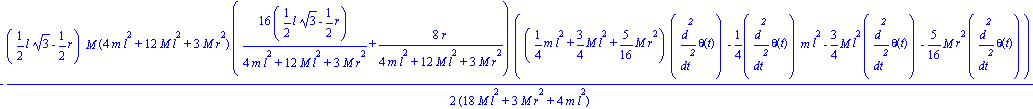
   Paso 9. Obtención de las ecuaciones de lagrange para las dos coordenadas generalizadas mediante el operador Ec_lag

>	ec_lagr();

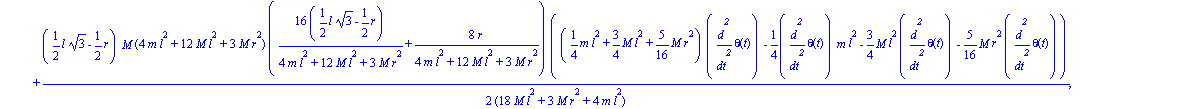
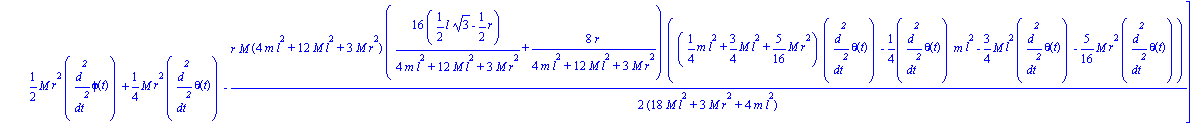
   Paso 10. Asignación de valores numéricos a los parámetros que queden sun asignar para poder proceder a la integración numérica.

>	g:=9.81:m:=5:M:=10:M2:=20:l:=8:r:=2:

   Paso 11. Integración numérica del problema mediante la función fint asignando el resultado a la variable res.

>	res:=fintr([0.1,1.,0.1,1.]);

>

res(1);

   Paso 12. Representación gráfica de las evoluciones temporales de la evolución temporal de theta mediante odeplot.

>	odeplot(res,[theta(t),t],0..4,color=red,numpoints=100);

>	odeplot(res,[phi(t),t],0..4,color=green,numpoints=100);

   Paso 13. Procedemos a realizar una animación del movimiento del conjunto por medio de la función dibu3.

>	dibu3(6.3,40);

>