ENUNCIADO DEL EJEMPLO 34
Sistema formado por un aro de masa M y radio R que se encuentra en un plano vertical liso y que tiene un punto de su periferia fijo en el centro de coordenadas y que puede girar respecto a él. El aro tiene ensartada una masa de valor m. Obtener las ecuaciones del movimiento.
Cargamos los paquetes de Maple que vamos a emplear, entre ellos el Mecapac3d, para lo cuál es necesario indicar previamente donde se encuentra la librería dentro del disco duro.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
El sistema tiene dos grados de libertad que asociamos con las coordenadas generalizadas theta y phi, que representan el giro de aro en el plano respecto a la normal al mismo y el ángulo que forma con la vertical descendente el radio que une el centro del aro con la partícula, respectivamente. Definimos dichas coordenadas generalizadas.
![cg := [theta, phi]](images/ejemplo34m_1.gif)
Definimos las coordenadas del centro de gravedad del aro y su matriz de rotación para definir después el aro. La matriz de rotación se consigue multiplicando por la izquierda las sucesivas matrices al representar giros absolutos.
| > |
xaro:=[0,sin(theta),-cos(theta)]: |
| > |
rotaro1:=rota(theta,1): |
| > |
rottot := evalm(rotaro1&*rotaro0) : |
Definimos el aro
| > |
a1:=[aro,xaro,rottot,maro,radaro]: |
Definimos a continuación las coordenadas de la partícula.
| > |
y:=sin(theta)+sin(phi): |
| > |
z:=-cos(theta)-cos(phi): |
Definimos la partícula.
| > |
p1:=[punto,x,y,z,mpto]: |
Definimos elementos gráficos para representar ángulos y los ejes.
| > |
angtheta:=[angulo,[0,0,-1],[0,0,0],[0,sin(theta),-cos(theta)],0.5]: |
| > |
angphi:=[angulo,[0,sin(theta),-cos(theta)-1],[0,sin(theta),-cos(theta)],[0,sin(theta)+sin(phi),-cos(theta)-cos(phi)],0.5]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,2,1],"Y"]: |
| > |
TZ := [texto,[0,0,2.1],"Z"]: |
| > |
ejey:=[segmento,[0,0,0],[0,1,0],green]: |
| > |
ejez:=[segmento,[0,0,0],[0,0,1],red]: |
Definimos el sistema, con los elementos gráficos incluidos.
| > |
sistema:=[TO,TY,TZ,ejey,ejez,a1,p1,angtheta,angphi]; |
![sistema := [[texto, [0, 0, -1],](images/ejemplo34m_2.gif)
![sistema := [[texto, [0, 0, -1],](images/ejemplo34m_3.gif)
![sistema := [[texto, [0, 0, -1],](images/ejemplo34m_4.gif)
Damos valores a los parámetros para poder representar el sistema en una situación determinada y poder realizar después la integración numérica.
| > |
maro:=1:g:=9.8:radaro:=1:mpto:=1: |
| > |
fG([evalf(Pi/2),evalf(Pi)]); |
![[Plot]](images/ejemplo34m_5.gif)
Calculamos la energía cinética y potencial del sistema, así como la Lagrangiana.
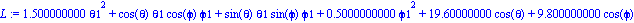
Ecuaciones del movimiento
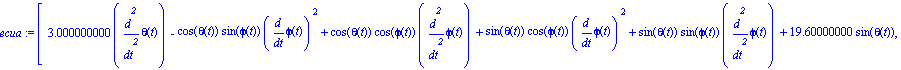
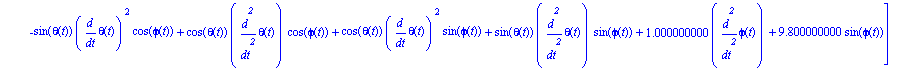
Realizamos la integración numérica indicando los valores iniciales de las coordenadas generalizadas y sus velocidades.
Gráfica de las coordenadas generalizadas en función del tiempo
| > |
odeplot(res,[t,phi(t)],0..1.65); |
| > |
odeplot(res,[t,theta(t)],0..1.65); |
![[Plot]](images/ejemplo34m_9.gif)
![[Plot]](images/ejemplo34m_10.gif)
Animación del movimiento
![[Plot]](images/ejemplo34m_11.gif)
![]()
![]()
![]()
![]()
![[Plot]](images/ejemplo34m_5.gif)
![]()
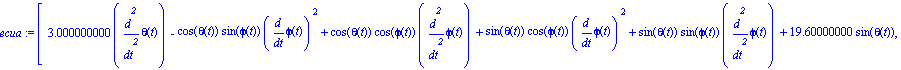
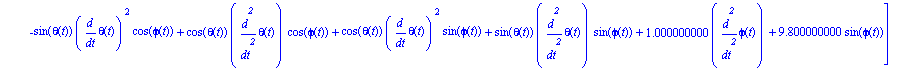
![[Plot]](images/ejemplo34m_9.gif)
![[Plot]](images/ejemplo34m_10.gif)
![[Plot]](images/ejemplo34m_11.gif)