ENUNCIADO DEL EJEMPLO 33
Sea un solido formado por una varilla de masa m1 y longitud l unida a un punto fijo O en uno de sus extremos. En el otro extremo tiene enganchado un disco de masa m2 y radio R. El solido puede girar libremente alrededor del punto O. Se pide hallar ecuaciones y representacion 3d del movimiento del solido y representacion grafica de los grados de libertad en funcion del tiempo con unas condiciones iniciales dadas.
Cargamos los paquetes de Maple que vamos a emplear, entre ellos el Mecapac3d, para lo cuál es necesario indicar previamente donde se encuentra la librería dentro del disco duro.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
El sistema tiene tres grados de libertad, que asociamos a las coordenadas generalizadas psi, theta y phi. Psi representael giro que realiza la varilla alrededor del eje Z, theta representa el giro de nutación de la varilla y phi el giro propio del disco.
![cg := [psi, theta, phi]](images/ejemplo33m_1.gif)
Dado que emplearemos un sistema de referencia móvil respecto al cuál referiremos la varilla y el disco, al definir la varilla no es necesario indicar una matriz de rotación propia. Esto es así porque el subsistema de referencia acompañará al sistema en su movimiento, siendo su eje Z el que va según la varilla, y los otros dos ejes contenidos en el plano del disco. Este subsistema no girará con el disco en su giro de precesión por lo que habrá que definirlo en la matriz de rotación del mismo. Definimos a continuación la varilla y el disco.
| > |
v1:=[varilla,[0,0,l/2],rota(0,1),m1,l]: |
| > |
d1:=[disco,[0,0,l],rota(phi,3),m2,R]: |
Definimos la matriz de rotación del subsistema respecto a los ejes fijos. El giro psi es absoluto, y el theta es relativo, por lo que el primero es por la izquierda y el segundo por la derecha en el producto. Definimos después el subsistema.
| > |
s1:=[subsistema2,[0,0,0],evalm(rottot),[v1,d1]]: |
Definimos a continuación elementos gráficos para representar los ejes del sistema inercial.
| > |
ejeY:=[vector,[0,0,0],[0,20,0],green]: |
| > |
ejeX:=[vector,[0,0,0],[20,0,0],red]: |
| > |
ejeZ:=[vector,[0,0,0],[0,0,20],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,20,1],"Y"]: |
| > |
TZ := [texto,[0,0,21],"Z"]: |
| > |
TX := [texto,[21,0,0],"X"]: |
Definimos el sistema global.
| > |
sistema:=[s1,ejeX,ejeY,ejeZ,TO,TX,TY,TZ]; |
![sistema := [[subsistema2, [0, 0, 0], matrix([[cos(psi), -sin(psi)*cos(theta), sin(psi)*sin(theta)], [sin(psi), cos(psi)*cos(theta), -cos(psi)*sin(theta)], [0, sin(theta), cos(theta)]]), [[varilla, [0,...](images/ejemplo33m_2.gif)
![sistema := [[subsistema2, [0, 0, 0], matrix([[cos(psi), -sin(psi)*cos(theta), sin(psi)*sin(theta)], [sin(psi), cos(psi)*cos(theta), -cos(psi)*sin(theta)], [0, sin(theta), cos(theta)]]), [[varilla, [0,...](images/ejemplo33m_3.gif)
![sistema := [[subsistema2, [0, 0, 0], matrix([[cos(psi), -sin(psi)*cos(theta), sin(psi)*sin(theta)], [sin(psi), cos(psi)*cos(theta), -cos(psi)*sin(theta)], [0, sin(theta), cos(theta)]]), [[varilla, [0,...](images/ejemplo33m_4.gif)
Calculamos la energía potencial del sistema y la cinética.
| > |
T:=simplify(fT(sistema)): |
La Lagrangiana del sistema
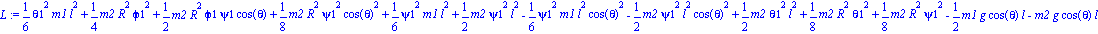
Ecuaciones del movimiento.
| > |
ecua:=map(simplify,ec_lag()); |

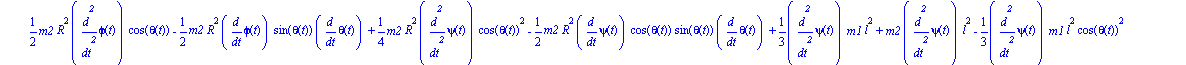
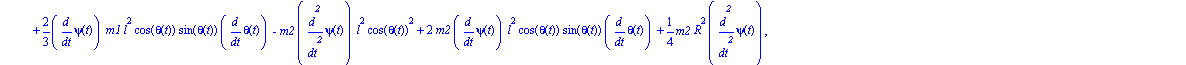
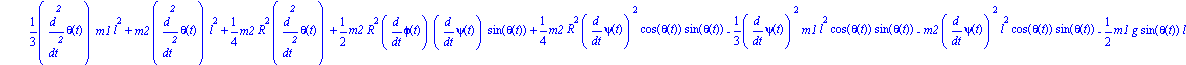


Damos valores a los parámetros para poder representar el sistema y realizar despuñes la integración numérica.
| > |
g:=9.8: m1:=10: m2:=5: R:=8: l:=20: |
| > |
fG([evalf(Pi/3),evalf(Pi/3),evalf(Pi/3)]); |
![[Plot]](images/ejemplo33m_12.gif)
Realizamos la integración numérica indicando los valores iniciales de las coordenadas generalizadas y sus velocidades.
| > |
res:= fint([0.1,10,0.4,1.5,0,9]): |
Animación del movimiento
![[Plot]](images/ejemplo33m_13.gif)
Gráfica de las coordenadas generalizadas en función del tiempo
| > |
odeplot(res,[t,psi(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo33m_14.gif)
| > |
odeplot(res,[t,theta(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo33m_15.gif)
| > |
odeplot(res,[t,phi(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo33m_16.gif)
![]()
![sistema := [[subsistema2, [0, 0, 0], matrix([[cos(psi), -sin(psi)*cos(theta), sin(psi)*sin(theta)], [sin(psi), cos(psi)*cos(theta), -cos(psi)*sin(theta)], [0, sin(theta), cos(theta)]]), [[varilla, [0,...](images/ejemplo33m_2.gif)
![]()
![sistema := [[subsistema2, [0, 0, 0], matrix([[cos(psi), -sin(psi)*cos(theta), sin(psi)*sin(theta)], [sin(psi), cos(psi)*cos(theta), -cos(psi)*sin(theta)], [0, sin(theta), cos(theta)]]), [[varilla, [0,...](images/ejemplo33m_4.gif)
![]()

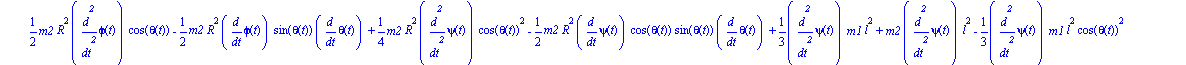
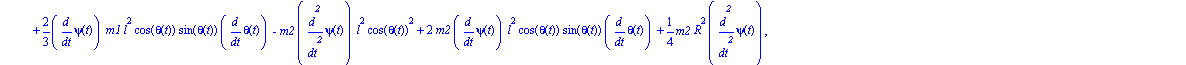
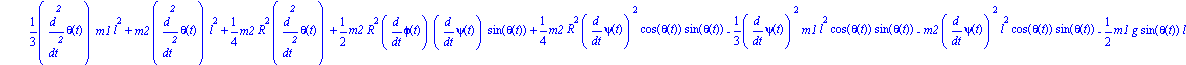
![]()

![[Plot]](images/ejemplo33m_12.gif)
![[Plot]](images/ejemplo33m_13.gif)
![[Plot]](images/ejemplo33m_14.gif)
![[Plot]](images/ejemplo33m_15.gif)
![[Plot]](images/ejemplo33m_16.gif)