ENUNCIADO DEL EJEMPLO 32
El sistema consta de dos masas puntuales m, unidas por una varilla rígida y sin masa de longitud a, y ensartadas con ligadura bilateral lisa en un aro de radio a y masa m. El aro tiene un diámetro vertical que permanece fijo, pudiendo girar alrededor del mismo. Se pide:
1. En la hipótesis de que el giro (theta punto) alrededor del eje vertical sea libre:
a) Ecuaciones diferenciales del movimiento
b) Integrales primeras en caso de haberlas
Cargamos los paquetes de Maple que vamos a emplear, entre ellos el mecapac3d, para lo cuál es necesario indicar la dirección en la que se encuentra en el disco duro.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
El sistema tiene dos grados de libertad, que relacionaré a las coordenadas generalizadas siguientes.
-theta: ángulo girado por el aro
-phi: ángulo que forma la perpendicular a la varilla que contiene a las masas con la vertical
![cg := [theta, phi]](images/ejemplo32m_1.gif)
Rotaciones necesarias para describir el movimiento:
Las definiré como rotaciones absolutas, por lo que su producto será por la izquierda en el caso del aro, mientras que las definiré como relativas en el caso de la varilla en cuanto al giro Phi, por lo que su producto será por la derecha.
| > |
rotar1:=rota(Pi/2,2):rotar2:=rota(-Pi/2+theta,3):rotARO:=evalm(rotar2&*rotar1): |
| > |
rotav1:=rota(phi+Pi/2,1):rotav2:=rota(-Pi/2+theta,3):rottv:=evalm(rotav2&*rotav1): |
Defino los elementos aro, varilla y partículas.
| > |
ar:=[aro,[0,0,0],rotARO,m,a]: |
| > |
var:=[varilla,[sqrt(3)*a*sin(phi)*cos(theta)/2,sqrt(3)*a*sin(phi)*sin(theta)/2,-sqrt(3)*a*cos(phi)/2],rottv,0,a]: |
| > |
p1:=[punto,(sqrt(3)*a*sin(phi)/2+a/2*cos(phi))*cos(theta),(sqrt(3)*a*sin(phi)/2+a/2*cos(phi))*sin(theta),(-sqrt(3)/2*a*cos(phi)+a/2*sin(phi)),m]: |
| > |
p2:=[punto,(sqrt(3)*a*sin(phi)/2-a/2*cos(phi))*cos(theta),(sqrt(3)*a*sin(phi)/2-a/2*cos(phi))*sin(theta),-(sqrt(3)/2*a*cos(phi)+a/2*sin(phi)),m]: |
Defino también elementos gráficos para representar los ejes, los ángulos y radios.
| > |
s1:=[segmento,[0,0,0],[sqrt(3)*a*sin(phi)*cos(theta)/2,sqrt(3)*a*sin(phi)*sin(theta)/2,-sqrt(3)*a*cos(phi)/2],red]: |
| > |
ejeY:=[vector,[0,0,0],[0,5,0],green]: |
| > |
ejeX:=[vector,[0,0,0],[5,0,0],red]: |
| > |
ejeZ:=[vector,[0,0,0],[0,0,5],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,5,1],"Y"]: |
| > |
TZ := [texto,[0,0,6],"Z"]: |
| > |
TX := [texto,[6,0,0],"X"]: |
| > |
a1:=[angulo,[1,0,4],[0,0,4],[cos(theta),sin(theta),4],1]: |
| > |
a2:=[angulo,[0,0,-1],[0,0,0],[sqrt(3)*a*sin(phi)*cos(theta)/2,sqrt(3)*a*sin(phi)*sin(theta)/2,-sqrt(3)*a*cos(phi)/2],1]: |
Definición de la varible sistema
| > |
sistema:=[ar,var,s1,ejeY,ejeX,ejeZ,TO,TX,TY,TZ,p1,p2,a1,a2]; |
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_2.gif)
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_3.gif)
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_4.gif)
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_5.gif)
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_6.gif)
Lagrangiana
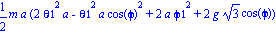
Ecuaciones de Lagrange
| > |
ecua:=ec_lag():simplify(ecua); |
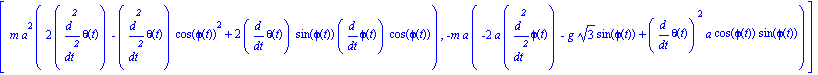
Como se ve al simplificar la expresión de la Lagrangiana, ésta solo depende explícitamente de la coordenada generalizada phi, por lo que existe una integral primera por la coordenada cíclica theta, que se corresponde con la conservación del momento cinético en la dirección vertical del sistema formado por las masas y el aro. Además, como el sistema es conservativo y sin movimientos impuestos, existe integral de Jacobi y coincide con la conservación de la energía (T+V).
| > |
integprim:=intprim():simplify(integprim); |
![[-m*theta1*a^2*(-2+cos(phi)^2)]](images/ejemplo32m_9.gif)
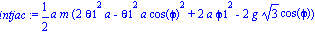
Introduzco unos valores para la representación
| > |
fG([evalf(Pi),evalf(Pi/3)]); |
![[Plot]](images/ejemplo32m_11.gif)
Impongo las condiciones iniciales e integro numerícamente
| > |
res:=fint([Pi/3,1,5*Pi/6,1]): |
Represento cómo varían en el tiempo las variables
| > |
odeplot(res,[t,theta(t)],0..20); |
![[Plot]](images/ejemplo32m_12.gif)
| > |
odeplot(res,[t,phi(t)],0..20); |
![[Plot]](images/ejemplo32m_13.gif)
Representación del movimiento:
![[Plot]](images/ejemplo32m_14.gif)
![]()
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_2.gif)
![]()
![]()
![]()
![sistema := [[aro, [0, 0, 0], rotARO, m, a], [varilla, [1/2*3^(1/2)*a*sin(phi)*cos(theta), 1/2*3^(1/2)*a*sin(phi)*sin(theta), -1/2*3^(1/2)*a*cos(phi)], rottv, 0, a], [segmento, [0, 0, 0], [1/2*3^(1/2)*...](images/ejemplo32m_6.gif)
![]()
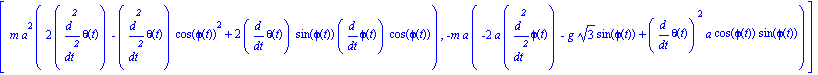
![]()
![]()
![[Plot]](images/ejemplo32m_11.gif)
![[Plot]](images/ejemplo32m_12.gif)
![[Plot]](images/ejemplo32m_13.gif)
![[Plot]](images/ejemplo32m_14.gif)