ENUNCIADO DEL EJEMPLO 30
Una varilla de masa m se halla ensartada en un aro circular de radio R por uno de sus extremos, pudiendo deslizar éste libremente sobre el aro, sometida a su propio peso. A su vez, al aro puede girar respecto de su diámetro vertical. Obtener las ecuaciones del movimiento.
Cargamos los paquetes que vamos a emplear.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
El sistema tiene tres grados de libertad, que quedan definidos con las coordenadas generalizadas siguientes: theta, phi, beta. Theta representa el giro del aro alrededor del eje z. Phi es el ángulo que nos indica la situación del extremo de la varilla en contacto con el aro. Beta es el ángulo girado por la varilla.
![cg := [theta, phi, beta]](images/ejemplo30m_1.gif)
Definimos a continuación el aro y la varilla, con las coordenadas de sus centro de gravedad y sus matrices de rotación. Para calcular las matrices de rotaciñon se han descompuesto en giros absolutos, de forma que las matrices se han multiplicado por la izquierda.
| > |
ar:=[aro,xg,rottot,m1,r]: |
| > |
rottot:=evalm(rot2&*rot1): |
| > |
va:=[varilla,[r*sin(phi)*cos(theta)+h/2*sin(beta)*cos(theta),r*sin(phi)*sin(theta)+h/2*sin(beta)*sin(theta),-r*cos(phi)-h/2*cos(beta)],rotvar,m2,h]: |
| > |
rotvar:=evalm(rot4&*rot3): |
Definimos a continuación elementos gráficos, como los ejes del sistema de referencia fijo o los ángulos.
| > |
a1:=[angulo,[0,0,-r],[0,0,0],[r*sin(phi)*cos(theta),r*sin(phi)*sin(theta),-r*cos(phi)],1]: |
| > |
s1:=[segmento,[0,0,0],[r*sin(phi)*cos(theta),r*sin(phi)*sin(theta),-r*cos(phi)],red]: |
| > |
ejeY:=[vector,[0,-r,0],[0,r,0],green]: |
| > |
ejeX:=[vector,[0,0,0],[r,0,0],red]: |
| > |
ejeZ:=[vector,[0,0,0],[0,0,r],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,r+1,1],"Y"]: |
| > |
TZ := [texto,[0,0,r+1],"Z"]: |
| > |
TX := [texto,[r+1,0,0],"X"]: |
| > |
ep:=[vector,[0,0,0],vector([7*cos(theta),7*sin(theta),0]),black]: |
| > |
v1:=[vector,[r*sin(phi)*cos(theta),r*sin(phi)*sin(theta),-r*cos(phi)],vector([2*cos(phi)*cos(theta),2*cos(phi)*sin(theta),2*sin(phi)]),green]: |
| > |
v2:=[vector,[r*sin(phi)*cos(theta),r*sin(phi)*sin(theta),-r*cos(phi)],vector([-2*sin(theta),2*cos(theta),0]),yellow]: |
Finalmente definimos el sistema con todos sus elementos.
| > |
sistema:=[ar,va,a1,ejeX,ejeY,ejeZ,TO,TX,TY,TZ,v1,v2,s1]; |
![sistema := [[aro, [0, 0, 0], rottot, m1, r], [varilla, [r*sin(phi)*cos(theta)+1/2*h*sin(beta)*cos(theta), r*sin(phi)*sin(theta)+1/2*h*sin(beta)*sin(theta), -r*cos(phi)-1/2*h*cos(beta)], rotvar, m2, h]...](images/ejemplo30m_2.gif)
![sistema := [[aro, [0, 0, 0], rottot, m1, r], [varilla, [r*sin(phi)*cos(theta)+1/2*h*sin(beta)*cos(theta), r*sin(phi)*sin(theta)+1/2*h*sin(beta)*sin(theta), -r*cos(phi)-1/2*h*cos(beta)], rotvar, m2, h]...](images/ejemplo30m_3.gif)
![sistema := [[aro, [0, 0, 0], rottot, m1, r], [varilla, [r*sin(phi)*cos(theta)+1/2*h*sin(beta)*cos(theta), r*sin(phi)*sin(theta)+1/2*h*sin(beta)*sin(theta), -r*cos(phi)-1/2*h*cos(beta)], rotvar, m2, h]...](images/ejemplo30m_4.gif)
![sistema := [[aro, [0, 0, 0], rottot, m1, r], [varilla, [r*sin(phi)*cos(theta)+1/2*h*sin(beta)*cos(theta), r*sin(phi)*sin(theta)+1/2*h*sin(beta)*sin(theta), -r*cos(phi)-1/2*h*cos(beta)], rotvar, m2, h]...](images/ejemplo30m_5.gif)
Calculamos ahora la energía cinética y la potencial para obtener así la Lagrangiana.
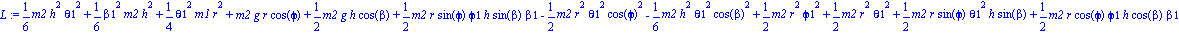
Ecuaciones del movimiento.

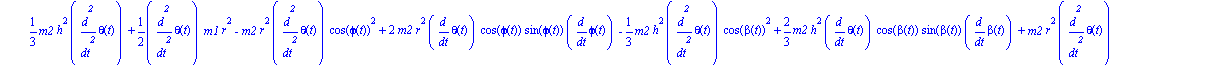
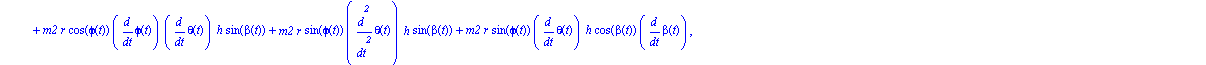
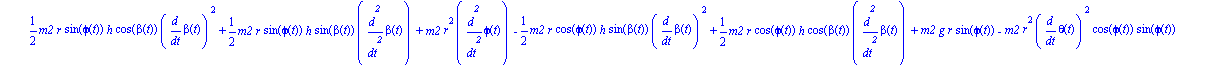

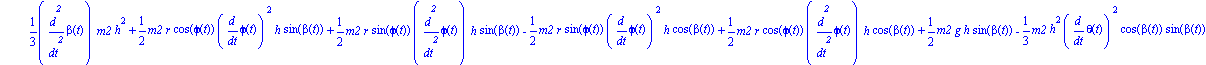

Damos valores a los parámetros que quedaban por indicar para obtener una representación del sistema en un instante determinado y para poder integrar numéricamente.
| > |
m1:=10: m2:=1: g:=9.81: r:=2: h:=3: |
| > |
fG([evalf(0),evalf(Pi/4),evalf(0)]); |
![[Plot]](images/ejemplo30m_14.gif)
Integración numérica dando los valores de las coordenadas y velocidades iniciales.
| > |
res:=fint([0,Pi,0,Pi,0,Pi]): |
Gráficas de las coordenadas en el tiempo y enfrentadas.
| > |
odeplot(res,[t,phi(t)],0..2.64); |
![[Plot]](images/ejemplo30m_15.gif)
| > |
odeplot(res,[t,theta(t)],0..2.64); |
![[Plot]](images/ejemplo30m_16.gif)
| > |
odeplot(res,[t,beta(t)],0..2.64); |
![[Plot]](images/ejemplo30m_17.gif)
| > |
odeplot(res,[theta(t),phi(t)],0..2.64); |
![[Plot]](images/ejemplo30m_18.gif)
| > |
odeplot(res,[theta(t),beta(t)],0..2.64); |
![[Plot]](images/ejemplo30m_19.gif)
| > |
odeplot(res,[beta(t),phi(t)],0..2.64); |
![[Plot]](images/ejemplo30m_20.gif)
Gráficos de las velocidades generalizadas en función del tiempo y enfrentadas.
| > |
odeplot(res,[t,diff(phi(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_21.gif)
| > |
odeplot(res,[t,diff(theta(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_22.gif)
| > |
odeplot(res,[t,diff(beta(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_23.gif)
| > |
odeplot(res,[theta(t),diff(phi(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_24.gif)
| > |
odeplot(res,[beta(t),diff(phi(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_25.gif)
| > |
odeplot(res,[phi(t),diff(theta(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_26.gif)
| > |
odeplot(res,[diff(beta(t),t),diff(theta(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_27.gif)
| > |
odeplot(res,[diff(phi(t),t),diff(theta(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_28.gif)
| > |
odeplot(res,[diff(beta(t),t),diff(phi(t),t)],0..2.64); |
![[Plot]](images/ejemplo30m_29.gif)
Animación del movimiento.
![[Plot]](images/ejemplo30m_30.gif)
![]()
![sistema := [[aro, [0, 0, 0], rottot, m1, r], [varilla, [r*sin(phi)*cos(theta)+1/2*h*sin(beta)*cos(theta), r*sin(phi)*sin(theta)+1/2*h*sin(beta)*sin(theta), -r*cos(phi)-1/2*h*cos(beta)], rotvar, m2, h]...](images/ejemplo30m_2.gif)
![]()
![]()
![sistema := [[aro, [0, 0, 0], rottot, m1, r], [varilla, [r*sin(phi)*cos(theta)+1/2*h*sin(beta)*cos(theta), r*sin(phi)*sin(theta)+1/2*h*sin(beta)*sin(theta), -r*cos(phi)-1/2*h*cos(beta)], rotvar, m2, h]...](images/ejemplo30m_5.gif)
![]()

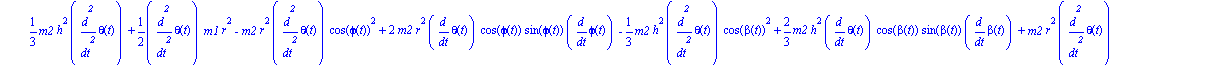
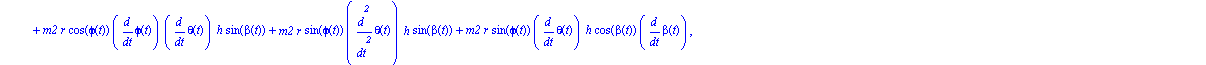
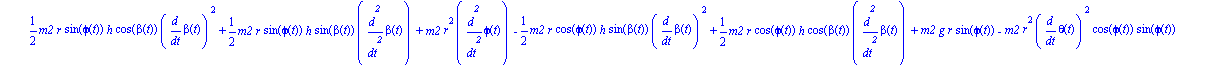
![]()
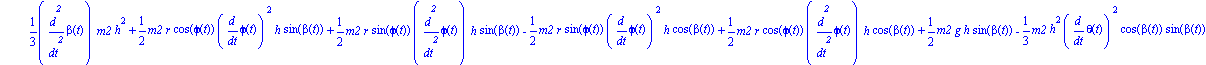

![[Plot]](images/ejemplo30m_14.gif)
![[Plot]](images/ejemplo30m_15.gif)
![[Plot]](images/ejemplo30m_16.gif)
![[Plot]](images/ejemplo30m_17.gif)
![[Plot]](images/ejemplo30m_18.gif)
![[Plot]](images/ejemplo30m_19.gif)
![[Plot]](images/ejemplo30m_20.gif)
![[Plot]](images/ejemplo30m_21.gif)
![[Plot]](images/ejemplo30m_22.gif)
![[Plot]](images/ejemplo30m_23.gif)
![[Plot]](images/ejemplo30m_24.gif)
![[Plot]](images/ejemplo30m_25.gif)
![[Plot]](images/ejemplo30m_26.gif)
![[Plot]](images/ejemplo30m_27.gif)
![[Plot]](images/ejemplo30m_28.gif)
![[Plot]](images/ejemplo30m_29.gif)
![[Plot]](images/ejemplo30m_30.gif)