ENUNCIADO EJEMPLO 3
    Un sólido está formado por un disco homogéneo y pesado de masa M y radio R al que se ha soldado en su centro (punto O) y perpendicularmente a su plano una varilla sin masa y de longitud muy grande.

    El sólido se mueve de forma que el punto O se encuentra contenido en todo momento en un una superficie cilindrica fija de eje vertical y radio R, y la varilla pasa siempre por un punto fijo P del eje de la superficie cilíndrica. La varilla esta soldada en un extremo al disco y en el otro posee un muelle o resorte que la une al punto P. Dicho muelle coarta su movimiento pero no modifica los grados de libertad del sistema. Se supone que no existe rozamiento en ninguna de las partes móviles.

   Paso 0. Reiniciación de las variables del sistema y llamada a los paquetes necesarios para las opeaciones.

>

restart;

    Cargamos los paquetes necesarios para nuestras operaciones, que son linalg, plots y plottools.

>	with(linalg):with(plots):with(plottools):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name changecoords has been redefined

Warning, the name arrow has been redefined

    Además de estos paquetes básicos será necesário cargar el paquete mecapac. Para ello deberemos indicar a Maple la situación de la librería. Dirección que será particular para cada ordenardor y debra comprobarse antes de continuar el proceso.

>	libname:="C:/",libname:

    Y se carga ahora mecapac como otro paquete cualquiera, una vez modificada la variable libname.

>	with(mecapac3d):

    El problema consiste en una especie de peonza que está constituida por un disco de radio R y una varilla. Además, la varilla lleva unida en un extremo al disco y el otro extremo a un muelle de rigidez k que la une al punto P (nuestro origen de ejes fijos) y que le coarta el movimiento. La varilla la consideramos sin masa y vamos a constituir el modelo de la peonza utilizando un sistema auxiliar (de ejes intermedios). Este sistema auxiliar lleva incluidos los giros correspondientes a la precesión y a la nutación.

    Paso 1. Definimos las coordenadas generalizadas del sistema en una lista que se denominará cg.

    Utilizaremos como coordenadas generalizadas los ángulos de Euler, precesión, nutación y rotación propia.

>	cg:= [psi,theta,phi];

    Paso 2. Definición mediante variables de los elementos que forman el sistema mecánico. Es decir, el disco, la varilla y el muelle.

Comenzamos definiendo el disco de radio R y masa M:

>	d1:=[disco,[0,0,R*cos(theta)/sin(theta)],rota(phi,3),M,R]:

    Posteriormente, definimos la varilla:

>	v1:=[varilla,[0,0,(R*cos(theta)/sin(theta))-(l/2)],evalm(rota(0,1)),0,l]:

    Y a continuación procedemos a definir el muelle:

>	m1:=[muelle,[0,0,-(l-R/sin(theta))],[0,0,0],K,z]:

    Paso 3. Definición de nuestros ejes coordenados que serán de dos tipos: móviles (ox, oy, oz), en minúsculas, y fijos (OX, OY, OZ), en mayúsculas. Estos ejes se definirán por medio de la variable vector.

>	ejex:=[vector,[0,0,0],[8,0,0],red]:

>	ejey:=[vector,[0,0,0],[0,8,0],green]:

>	ejez:=[vector,[0,0,0],[0,0,8],blue]:

>	TO:=[texto,[1,1,0],"O"]:

>	TX:=[texto,[10,1,0],"X"]:

>	TY:=[texto,[1,10,0],"Y"]:

>	TZ:=[texto,[0,0,11],"Z"]:

>	ejeX:=[vector,[0,0,0],[10,0,0],red]:

>	ejeY:=[vector,[0,0,0],[0,10,0],green]:

>	ejeZ:=[vector,[0,0,0],[0,0,10],blue]:

    Paso 4. Definición de la variable sistema que contiene una lista con los elementos anteriormente definidos y, en nuestro caso, del subsistema auxiliar en el que irán referidos todos los elementos del problema.

>	s1:=[subsistema2,[0,0,0],evalm(rota(psi,3)&*rota(theta,1)),[d1,m1,v1,ejex,ejey,ejez]]:

>	sistema:=[s1,ejeX,ejeY,ejeZ,TX,TY,TZ,TO]:

    Paso 5. Obtención de la energía cinética del sistema mediante fT asignándola a una variable que se denominará T.

>	T:=fT(sistema);

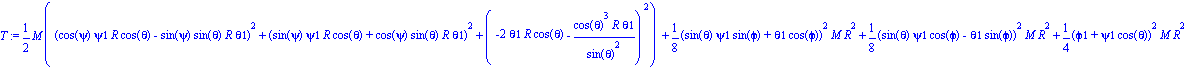
    Paso 6. Obtención de la energía potencial del sistema mediante fV asignándola a una variable que se denominará V.

>	V:=fV(sistema);

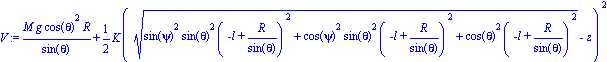
    Paso 7. Obtención de la lagrangiana, como diferencia entre la energía cinética y la potencial, que se debe denominar L.

>	L:=simplify(T-V);

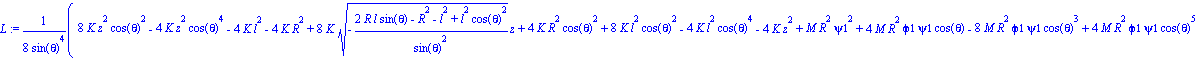
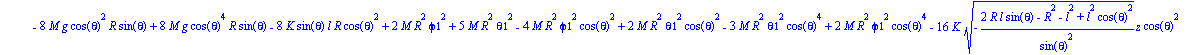
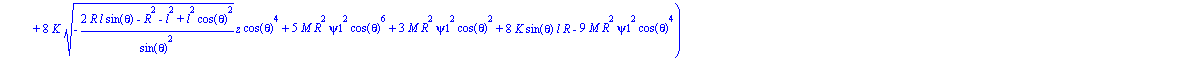
    Paso 8. Obtención de las ecuaciones de Lagrange por medio de la función ec_l para cada una de las coordenadas generalizadas de nuestro sistema.

    Así, para la variable psi:

>	ecua1:=map(ec_l,psi);

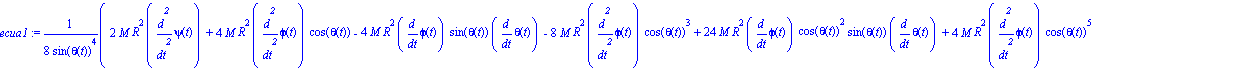
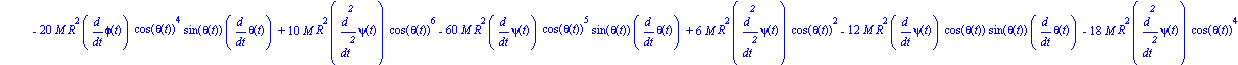
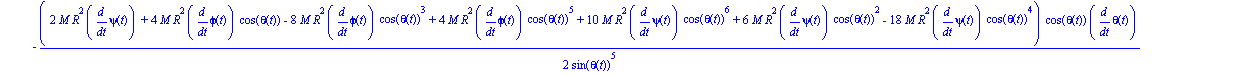
    De la misma forma, para theta:

>	ecua2:=map(ec_l,theta);

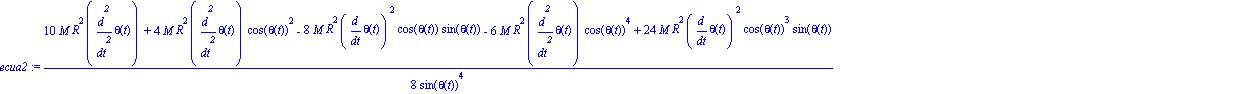
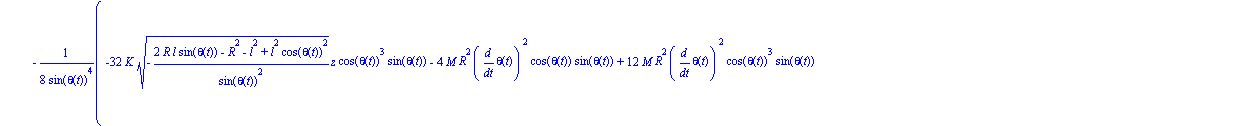
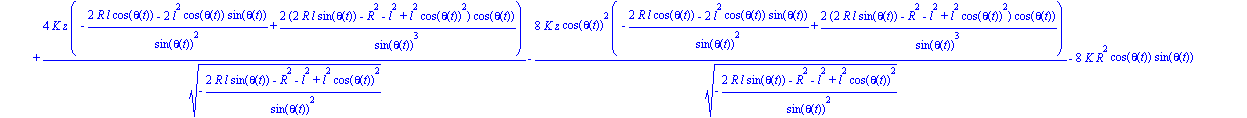
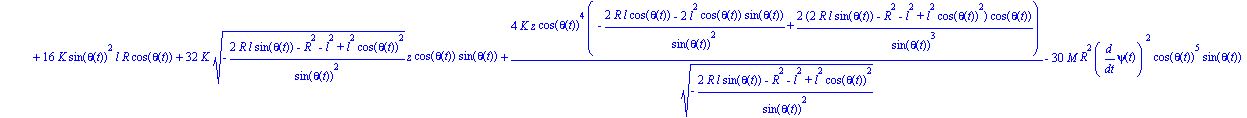
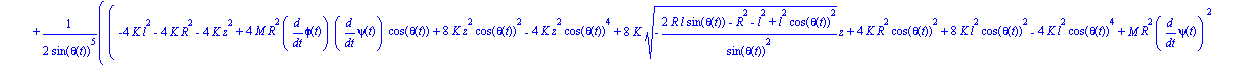
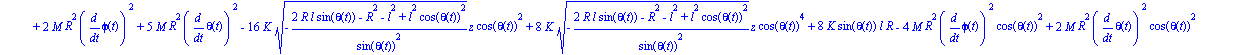
    Y finalmente para phi:

>	ecua3:=map(ec_l,phi);

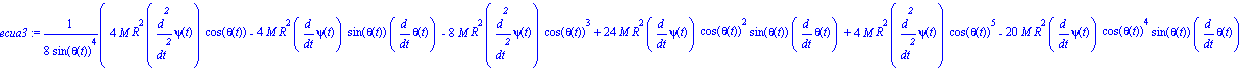
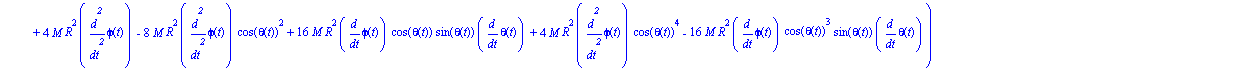
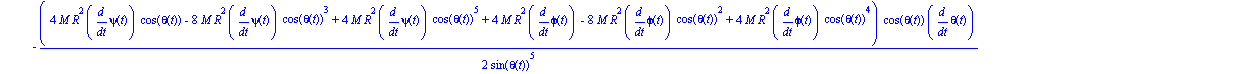
    Paso 9. Asignación de valores numéricos a los parámetros que queden sin asignar para poder proceder a la integración.

>	M:=1: g:=9.8: R:=3: K:=10000: l:=10: z:=0:

    Paso 10. Integración numérica del problema mediante la función fint asignando el resultado a la variable res.

>	res:=fint([1.,2.,1.,2.,1.,2.]);

    Paso 11. Representación gráfica de las evoluciones temporales de cada variable mediante odeplot.

Primero representamos los valores que adoptará la función theta(t) respecto a los valores de t comprendidos entre 0 y 2.

>	p1:=odeplot(res,[t,theta(t)],0..2,color=red,numpoints=100):

>	p2:=odeplot(res,[t,psi(t)],0..2.,color=green,numpoints=100):

>	p3:=odeplot(res,[t,phi(t)],0..2.,color=blue,numpoints=100):

>	display({p1,p2,p3});

    Paso 12 y último. Procedemos a realizar una animación del movimiento de todo el conjunto con la función dibu3 pues nuestra lagrangiana no depende del tiempo de forma explícita. La función dibu3 realizará esta animación de los resultados acumulados en la variable res para una duración de 6 segundos y 70 imágenes.

>	dibu3(6,70);

>