ENUNCIADO DEL EJEMPLO 29
Sea el sistema formado por un aro de radio R y masa M que está restringido siempre en un plano vertical y que puede girar sólo alrededor del eje z. Tiene ensartada una partícula de masa m que a su vez está unida a una varilla sin masa de longitud R que está en todo momento en el plano del aro y perpendicular al mismo, de forma que une el centro del aro con la partícula. Dicho extremo de la varilla coincidente con el centro del aro está unido, por medio de un muelle de longitud natural nula y constante k, con el centro de coordenadas. Se pide obtener las ecuaciones del movimiento.
Cargamos los paquetes de Maple que vamos a emplear, entre ellos, el mecapac, para lo cuál es necesario indicar la carpeta en la que se encuentra la librería.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
El sistema tiene tres grados de libertad que asociaremos a las coordenadas generalizadas phi, theta y z. Phi representa el giro alrededor de la vertical que realiza el plano en el que se encuentra el sistema. Theta representa el ángulo que forma con la horizontal del plano el radio que une el centro del aro con la partícula. Z representa la coordenada z del centro del aro.
![cg := [phi, theta, z]](images/ejemplo29m_1.gif)
Definimos ahora el aro, a partir de las coordenadas de su centro de gravedad y la matriz de rotación que obtenemos mediante producto de matrices que representan giros absolutos.
| > |
rot:=evalm(rota(phi,3)&*rota(Pi/2,2)): |
Definimos la partícula y el segmento (o varilla sin masa) que la une con el centro del aro. Definimos a continuación el muelle de longitud natural nula.
| > |
p1:=[punto,-R*cos(theta)*sin(phi),R*cos(theta)*cos(phi),z-R*sin(theta),m]: |
| > |
s1:=[segmento,[0,0,z],[-R*cos(theta)*sin(phi),R*cos(theta)*cos(phi),z-R*sin(theta)],green]: |
| > |
m1:=[muelle,[0,0,0],[0,0,z],k,0]: |
Definimos también unos elementos gráficos para representar los ejes del sistema fijo.
| > |
ejeY:=[vector,[0,0,0],[0,2,0],green]: |
| > |
ejeX:=[vector,[0,0,0],[2,0,0],red]: |
| > |
ejeZ:=[vector,[0,0,0],[0,0,2],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,1.5,1],"Y"]: |
| > |
TZ := [texto,[0,0,2.1],"Z"]: |
| > |
TX := [texto,[2.1,0,0],"X"]: |
Definimos el sistema global ocn todos sus elementos, incluidos los gráficos.
| > |
sistema:=[a1,p1,s1,m1,ejeY,ejeX,ejeZ,TO,TX,TY,TZ]; |
![sistema := [[aro, [0, 0, z], rot, M, R], [punto, -R*cos(theta)*sin(phi), R*cos(theta)*cos(phi), z-R*sin(theta), m], [segmento, [0, 0, z], [-R*cos(theta)*sin(phi), R*cos(theta)*cos(phi), z-R*sin(theta)...](images/ejemplo29m_2.gif)
![sistema := [[aro, [0, 0, z], rot, M, R], [punto, -R*cos(theta)*sin(phi), R*cos(theta)*cos(phi), z-R*sin(theta), m], [segmento, [0, 0, z], [-R*cos(theta)*sin(phi), R*cos(theta)*cos(phi), z-R*sin(theta)...](images/ejemplo29m_3.gif)
![sistema := [[aro, [0, 0, z], rot, M, R], [punto, -R*cos(theta)*sin(phi), R*cos(theta)*cos(phi), z-R*sin(theta), m], [segmento, [0, 0, z], [-R*cos(theta)*sin(phi), R*cos(theta)*cos(phi), z-R*sin(theta)...](images/ejemplo29m_4.gif)
Damos un valor al radio para realizar un gráfico del sistema en un instante determinado y comprobar que se definió bien.
| > |
fG([evalf(0),evalf(Pi/4),evalf(0)]); |
![[Plot]](images/ejemplo29m_5.gif)
Volvemos a dejar el radio como una constante sin valor para poder obtener las ecuaciones de una forma más genérica.
Obtenemos la Lagrangiana a partir de la energía potencial y cinética.
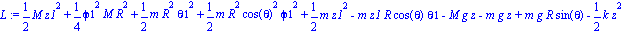
Ecuaciones del movimiento
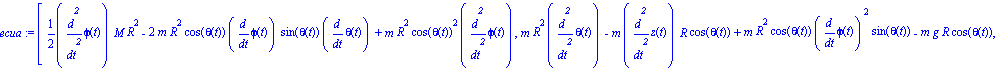
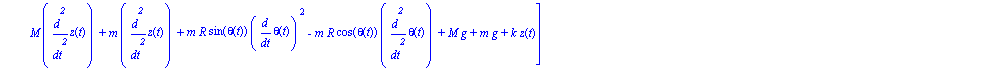
Damos ahora valores a los parámetros para poder realizar la integración numérica y obtener así las gráficas que representan las coordenadas generalizadas en el tiempo y una animación del movimiento.
| > |
M:=2:m:=1:R:=1:k:=15:g:=9.8: |
Para realizar la integración numérica es necesario indicar los valores iniciales de las coordenadas generalizadas así como de las velocidades.
| > |
res:=fint([0,1,Pi/2,5,0,5]): |
| > |
odeplot(res,[t,phi(t)],0..5); |
![[Plot]](images/ejemplo29m_9.gif)
| > |
odeplot(res,[t,theta(t)],0..5); |
![[Plot]](images/ejemplo29m_10.gif)
Animación del movimiento durante 4 segundos con 50 imágenes.
![[Plot]](images/ejemplo29m_11.gif)
![]()
![]()
![]()
![]()
![[Plot]](images/ejemplo29m_5.gif)
![]()
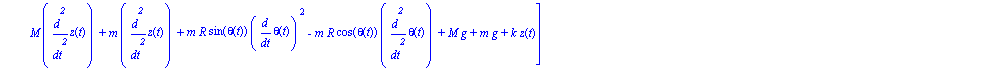
![[Plot]](images/ejemplo29m_9.gif)
![[Plot]](images/ejemplo29m_10.gif)
![[Plot]](images/ejemplo29m_11.gif)