ENUNCIADO DEL EJEMPLO 27
Un sólido homogéneo de masa m se compone de un semiaro de centro O y radio a y una varilla de longitud 2a coincidente con el diámetro. El punto O permanece fijo en el origen de coordenadas, y la varilla se mantiene en todo momento en el plano horizontal, sobre el cual desliza. Además, el punto medio del semiaro está unido mediante un resorte lineal de constante k y longitud natural l a un punto fijo que se encuentra en la vertical de O, a una altura a.
Cargamos los paquetes de Maple que vamos a emplear.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
Definimos las coordenadas generalizadas, que en este caso son dos, al tener el sistema dos grados de libertad. Las coordenadas que usaremos serán psi y theta para representar la nutación y la precesión.
![cg := [psi, theta]](images/ejemplo27m_1.gif)
A continuación definimos las coordenadas de los centros de masas de la varilla (punto O, fijo) y del semiaro.
| > |
xgs:=[(2*a/Pi)*cos(theta)*(-sin(psi)),(2*a/Pi)*cos(theta)*cos(psi),(2*a/Pi)*sin(theta)]: |
Se trata de un sólido homogéneo, así que las masas de la varilla y el semiaro por separado serán, respectivamente:
Ahora calculamos las matrices de rotación de cada sólido, teniendo en cuenta que hemos empleado giros absolutos, por lo que multiplicamos las matrices por la izquierda.
| > |
rotv:=evalm(rota(psi,3)&*rota(theta,1)&*rota(Pi/2,2)): |
| > |
rots:=evalm(rota(psi,3)&*rota(theta,1)): |
Y por último definimos totalmente el sistema con todos sus elementos: sólido (compuesto por varilla y semiaro), muelle, y sistema de coordenadas fijo.
| > |
v1:=[varilla,xgv,rotv,mv,2*a]: |
| > |
s1:=[semiaro,xgs,rots,ms,a]: |
| > |
m1:=[muelle,[0,0,a],[-a*cos(theta)*sin(psi),a*cos(theta)*cos(psi),a*sin(theta)],k,l]: |
| > |
ejeY:=[vector,[0,0,0],[0,2,0],green]: |
| > |
ejeX:=[vector,[0,0,0],[2,0,0],red]: |
| > |
ejeZ:=[vector,[0,0,0],[0,0,2],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,2,1],"Y"]: |
| > |
TZ := [texto,[0,0,2.5],"Z"]: |
| > |
TX := [texto,[2.5,0,0],"X"]: |
| > |
sistema:=[v1,s1,m1,ejeX,ejeY,ejeZ,TO,TX,TY,TZ]; |
![sistema := [[varilla, [0, 0, 0], rotv, 2*m/(2+Pi), 2*a], [semiaro, [-2*a*cos(theta)*sin(psi)/Pi, 2*a*cos(theta)*cos(psi)/Pi, 2*a*sin(theta)/Pi], rots, m*Pi/(2+Pi), a], [muelle, [0, 0, a], [-a*cos(thet...](images/ejemplo27m_2.gif)
![sistema := [[varilla, [0, 0, 0], rotv, 2*m/(2+Pi), 2*a], [semiaro, [-2*a*cos(theta)*sin(psi)/Pi, 2*a*cos(theta)*cos(psi)/Pi, 2*a*sin(theta)/Pi], rots, m*Pi/(2+Pi), a], [muelle, [0, 0, a], [-a*cos(thet...](images/ejemplo27m_3.gif)
![sistema := [[varilla, [0, 0, 0], rotv, 2*m/(2+Pi), 2*a], [semiaro, [-2*a*cos(theta)*sin(psi)/Pi, 2*a*cos(theta)*cos(psi)/Pi, 2*a*sin(theta)/Pi], rots, m*Pi/(2+Pi), a], [muelle, [0, 0, a], [-a*cos(thet...](images/ejemplo27m_4.gif)
Calculamos la función lagrangiana, calculando antes sus componentes.
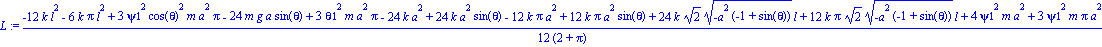
Y obtenemos las dos ecuaciones diferenciales de movimiento:
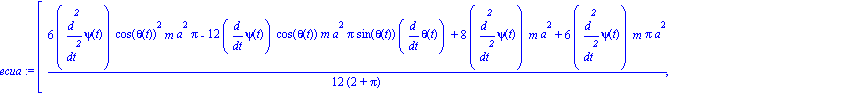
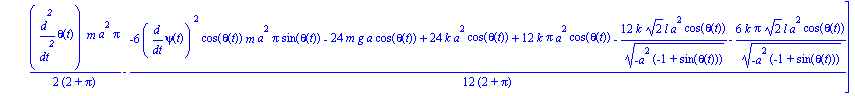
Para poder resolver el sistema de ecuaciones obtenido, primero hay que dar valores numéricos a m, a, k, l y g (aceleración de la gravedad).
En primer lugar, veamos un caso en el que el muelle tiene longitud natural nula. Obtenemos las gráficas de las coordenadas generalizadas en el tiempo y la animación.
| > |
a:=1:m:=1:g:=9.8:k:=4:l:=0: |
| > |
res:=fint([0,0.1,-Pi/4,0]); |

| > |
odeplot(res,[t,psi(t)],0..20); |
![[Plot]](images/ejemplo27m_9.gif)
| > |
odeplot(res,[t,theta(t)],0..20); |
![[Plot]](images/ejemplo27m_10.gif)
![[Plot]](images/ejemplo27m_11.gif)
En segundo lugar, veamos otro caso en el que la longitud natural del muelle no es nula. Obtenemos las gráficas de las coordenadas generalizadas en el tiempo y la animación.
| > |
a:=1:m:=1:g:=9.8:k:=5.8:l:=0.5: |
| > |
res:=fint([0,0.1,-Pi/3,0]); |

| > |
odeplot(res,[t,psi(t)],0..20); |
![[Plot]](images/ejemplo27m_13.gif)
| > |
odeplot(res,[t,theta(t)],0..20); |
![[Plot]](images/ejemplo27m_14.gif)
![[Plot]](images/ejemplo27m_15.gif)
![]()
![sistema := [[varilla, [0, 0, 0], rotv, 2*m/(2+Pi), 2*a], [semiaro, [-2*a*cos(theta)*sin(psi)/Pi, 2*a*cos(theta)*cos(psi)/Pi, 2*a*sin(theta)/Pi], rots, m*Pi/(2+Pi), a], [muelle, [0, 0, a], [-a*cos(thet...](images/ejemplo27m_2.gif)
![]()
![sistema := [[varilla, [0, 0, 0], rotv, 2*m/(2+Pi), 2*a], [semiaro, [-2*a*cos(theta)*sin(psi)/Pi, 2*a*cos(theta)*cos(psi)/Pi, 2*a*sin(theta)/Pi], rots, m*Pi/(2+Pi), a], [muelle, [0, 0, a], [-a*cos(thet...](images/ejemplo27m_4.gif)
![]()
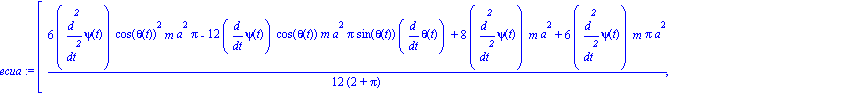
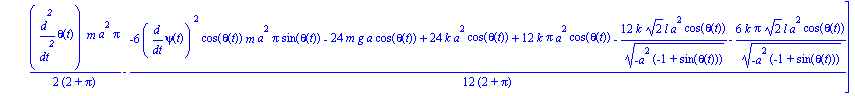
![]()
![[Plot]](images/ejemplo27m_9.gif)
![[Plot]](images/ejemplo27m_10.gif)
![[Plot]](images/ejemplo27m_11.gif)
![]()
![[Plot]](images/ejemplo27m_13.gif)
![[Plot]](images/ejemplo27m_14.gif)
![[Plot]](images/ejemplo27m_15.gif)