ENUNCIADO DEL EJEMPLO 25
Sea el sistema formado por un semiaro que tiene un extremo fijo en el origen de coordenadas y cuyo otro extremo está obligado a deslizar en el plano coordenado (x,y), y por una partícula que se encuentra ensartada en el semiaro. El semiaro tiene radio R y masa M, y la partícula tiene masa m. Se pide obtener las ecuaciones del movimiento y la animación del mismo.
Comenzamos cargando los paquetes de Maple que vamos a necesitar, así como el Mecapac3d, para lo cuál será necesario indicar donde se encuentra la librería mecapac en el disco duro.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
El sistema formado por la partícula y el semiaro tiene tres grados de libertad, ya que: el semiaro tendría inicialmente seis, pero la restricción de que un extremo esté fijo en el origen de coordenadas supone dos tres condiciones (Xext = Yext = Zext = 0), y la otra condición del otro extremo supone una nueva ecuación (Zotroext = 0). Por lo tanto, el semiaro tendría dos grados de libertad. La partícula tendría tres grados de libertad iniciales, pero como se encuentra ensartada en el semiaro, con una única coordenada generalizada tendríamos su posición relativa en el semiaro, y con la de semiaro, su posición global. Por lo tanto, como el sistema tiene tres grados de libertad, emplearemos tres coordenadas generalizadas para definirlo, que serán [beta, theta,phi]. Las dos primeras son angulares y nos sirven para definir la posición del semiaro, y la última es también angular y nos define la posición de la partícula en el semiaro. Definimos dichas coordenadas generalizadas.
Definimos ahora los elementos del sistema, comenzando por el semiaro. Para indicar la posición de su centro de gravedad realizaremos la suma de dos vectores que nos lleven a él, siendo el primero el que une el origen con el centro aro completo, y el otro vector el que une dicho punto con el centro de gravedad del semiaro. Para obtener la matriz de rotación del semiaro realizamos el producto de las matrices que representan los sucesivos giros que hay que dar para ir de los ejes propios a los fijos, considerando que si los giros se refieren a ejes propios, la multiplicación se realiza por la derecha, mientras que si el giro es absoluto, se multiplican por la izquierda.
| > |
vec1:=[R*cos(beta),R*sin(beta),0]: |
| > |
vec2:=[-2*R/Pi*sin(theta)*sin(beta),2*R/Pi*sin(theta)*cos(beta),-2*R/Pi*cos(theta)]: |
| > |
rtot:=evalm(r2&*r3 &* r1): |
| > |
saro:=[semiaro,cgsemiaro,rtot,M,R]: |
Definimos la partícula, habiendo calculado a parte la expresión de las coordenadas de la misma en función de los grados de libertad.
| > |
par:=[punto,-sin(phi)*sin(theta)*sin(beta)+cos(phi)*cos(beta)+cos(beta),sin(phi)*sin(theta)*cos(beta)+cos(phi)*sin(beta)+sin(beta),-sin(phi)*cos(theta),m]: |
Definimos también elementos gráficos para representar el sistema de referencia fijo.
| > |
ejeY:=[vector,[0,0,0],[0,5,0],green]: |
| > |
ejeX:=[vector,[0,0,0],[5,0,0],red]: |
| > |
ejeZ:=[vector,[0,0,0],[0,0,5],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,5,1],"Y"]: |
| > |
TZ := [texto,[0,0,6],"Z"]: |
| > |
TX := [texto,[5,0,1],"X"]: |
Definimos el sistema, indicando todos sus elementos, incluidos los gráficos.
| > |
sistema:=[saro,ejeX,ejeY,ejeZ,TO,TY,TX,TZ,par]; |
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_1.gif)
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_2.gif)
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_3.gif)
Damos valor al radio para poder representar una situación del sistema.
| > |
fG([evalf(Pi/4),evalf(Pi/4),evalf(Pi/2)]); |
![[Plot]](images/ejemplo25m_4.gif)
Volvemos a nombrar el radio como una constante sin valor para obterner las ecuaciones del movimiento de uina forma más genérica.
Calculamos a continuación la energía cinética, la potencial y la Lagrangiana del sistema.
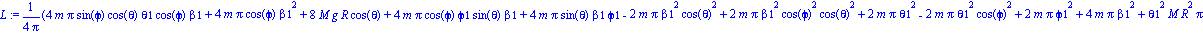

Obtenemos ahora las tres ecuaciones del movimiento.
| > |
ecua:=simplify(ec_lag()); |

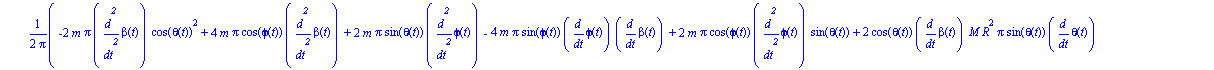
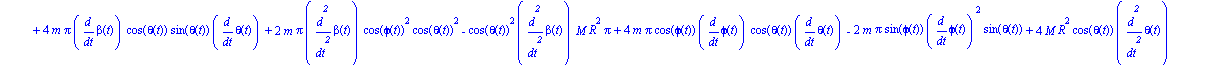
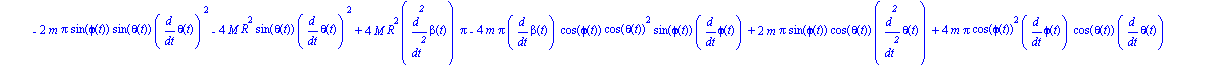
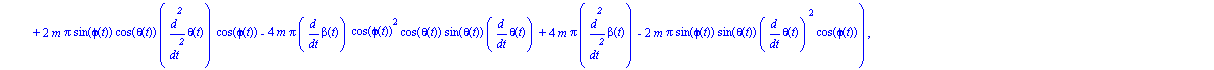
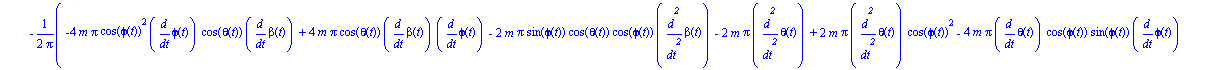
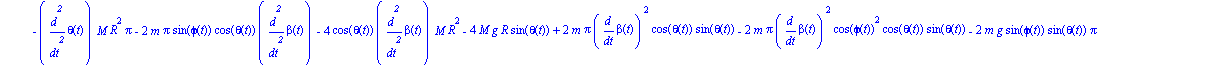

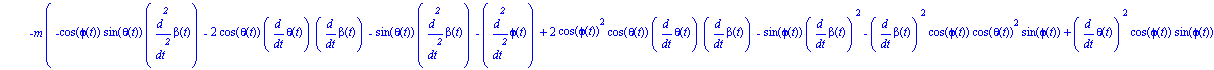

Damos valor a todos los parámetros para realizar la integración numérica, para la cuál será necesario indicar unos valores de las coordenadas generalizadas y sus velocidades en el instante inicial.
| > |
M:=2: m:=1: g:=9.8: R:=1: |
| > |
res:=fint([evalf(Pi/4),0,evalf(Pi/4),3.4,evalf(Pi/2),0]): |
Animación del movimiento durante 4 segundos con 40 imágenes.
![[Plot]](images/ejemplo25m_17.gif)
Gráficas de las coordenadas generalizadas en función del tiempo.
| > |
odeplot(res,[t,theta(t)],t=0..2,numpoints=100,color=blue); |
![[Plot]](images/ejemplo25m_18.gif)
| > |
odeplot(res,[t,beta(t)],t=0..2,numpoints=100,color=blue); |
![[Plot]](images/ejemplo25m_19.gif)
| > |
odeplot(res,[t,phi(t)],t=0..2,numpoints=100,color=blue); |
![[Plot]](images/ejemplo25m_20.gif)
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_1.gif)
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_3.gif)
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_1.gif)
![]()
![sistema := [[semiaro, [-2*R*sin(theta)*sin(beta)/Pi+R*cos(beta), 2*R*sin(theta)*cos(beta)/Pi+R*sin(beta), -2*R*cos(theta)/Pi], rtot, M, R], [vector, [0, 0, 0], [5, 0, 0], red], [vector, [0, 0, 0], [0,...](images/ejemplo25m_3.gif)
![[Plot]](images/ejemplo25m_4.gif)
![]()
![]()

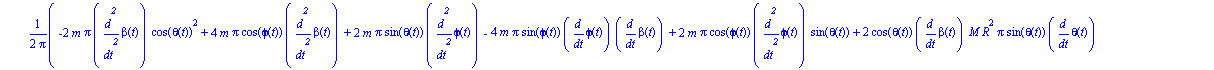
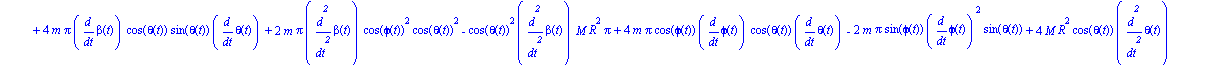
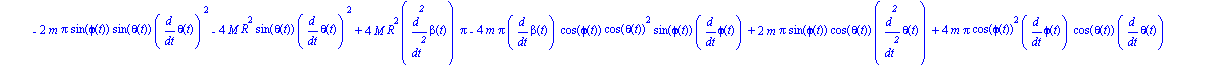
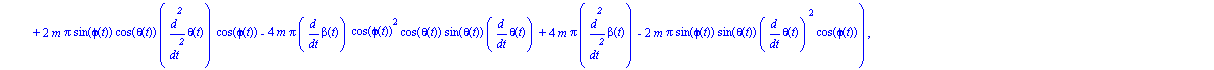
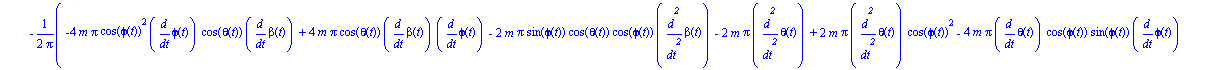
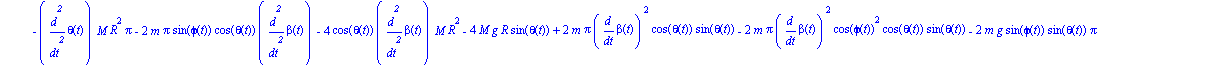

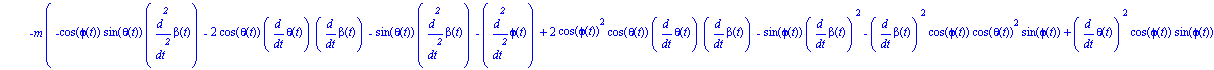

![[Plot]](images/ejemplo25m_17.gif)
![[Plot]](images/ejemplo25m_18.gif)
![[Plot]](images/ejemplo25m_19.gif)
![[Plot]](images/ejemplo25m_20.gif)