Se dispone de un semiaro de masa M y radio R . En su punto más bajo hay unido un muelle de constante k y longitud natural l, estando el otro extremo del muelle en el suelo(en el origen de coordenadas).El centro de gravedad del semiaro se mueve en todo momento segun el eje z. El semiaro puede girar alrededor del eje z. Sobre el semiaro, y en su mismo plano, se mueve un disco de masa m y radio r,que rueda sin deslizar. Obtener las ecuaciones del movimiento del sistema.
Cargamos los paquetes de Maple que vamos a necesitar.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
Indicamos el directorio en el que se encuentra la librería mecapac3d y lo cargamos.
| > |
libname:="C:\",libname: |
El sistema formado por el semiaro y disco tiene tres grados de libertad. Los identificamos con las coordenadas generalizadas theta, phi y z, que representan, respectivamente, el ángulo que forma con la vertical el radiovector que une el centro del semiaro con el centro de gravedad del disco, el giro del semiaro alrededor de la vertical, y la coordenada z del punto más bajo del semiaro. Con estas tres coordenadas generalizadas queda definida la posición de todos los elementos del sistema en cualquier instante de tiempo.
![cg := [theta, phi, z]](images/ejercicio18m_1.gif)
Definimos ahora el semiaro, obteniendo primero la posición del centro de gravedad y la matriz de rotación entre los ejes fijos y los ejes propios. Para obtener la matriz de rotación realizamos el producto por la izquierda, ya que los sucesivos giros que se realizan al semiaro para llevarlo a su posición final son giros absolutos, referidos al sistema de referencia de ejes fijos.
| > |
xgvar1:=[0,0,z+R-2*R/Pi]: |
| > |
rotp:=evalm(rotp4&*rotp2&* rotp1): |
| > |
m1:=[semiaro,xgvar1,rotp,M,R]; |
![m1 := [semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R]](images/ejercicio18m_2.gif)
De la misma forma, definimos el disco, indicando las coordenadas de su centro de gravedad en función de las coordenadas generalizadas, así como la matriz de rotación, teniendo en cuenta que el disco rueda sin deslizar.
| > |
xgvar2:=[-(R-r)*sin(theta)*sin(phi),(R-r)*sin(theta)*cos(phi),z+R-(R-r)*cos(theta)]: |
| > |
rotp7:=rota(-R/r*theta,1): |
| > |
rotdisco:=evalm(rotp6&*rotp7&*rotp3): |
| > |
m2:=[disco,xgvar2,rotdisco,m,r]; |
![m2 := [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r]](images/ejercicio18m_3.gif)
A continuación definimos el muelle, indicando sus dos extremos, su constante y su longitud natural.
| > |
c1:=[muelle,x1,x2,k,l]; |
![c1 := [muelle, [0., 0., 0.], [0., 0., z], k, l]](images/ejercicio18m_4.gif)
También incorporamos al sistema unos elementos gráficos para visualizarlo mejor. Los elementos son segmentos para representar los ejes, dos ángulos que simbolicen las coordenadas generalizadas phi y theta, y textos que nombren los ejes.
| > |
ejex:=[segmento,[0,0,0],[15,0,0],red]: |
| > |
ejey:=[segmento,[0,0,0],[0,15,0],blue]: |
| > |
ejez:=[segmento,[0,0,0],[0,0,15],green]: |
| > |
antheta:=[angulo,[0,0,z],[0,0,z+R],[-(R-r)*sin(theta)*sin(phi),(R-r)*sin(theta)*cos(phi),z+R-(R-r)*cos(theta)],R/2]: |
| > |
anphi:=[angulo,[0,R,z+R],[0,0,z+R],[-R*sin(phi),R*cos(phi),z+R],R/2]: |
| > |
textox:=[texto,[15,2,0],"X"]: |
| > |
textoy:=[texto,[2,15,0],"Y"]: |
| > |
textoz:=[texto,[2,2,15],"Z"]: |
A continuación, definimos el sistema, indicando todos los elementos que lo conforman.
| > |
sistema:=[m1,m2,c1,ejex,ejey,ejez,antheta,anphi,textox,textoy,textoz]; |
![sistema := [[semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R], [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r], [muelle, [0., 0., 0.], [0., 0., z], k, l]...](images/ejercicio18m_5.gif)
![sistema := [[semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R], [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r], [muelle, [0., 0., 0.], [0., 0., z], k, l]...](images/ejercicio18m_6.gif)
![sistema := [[semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R], [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r], [muelle, [0., 0., 0.], [0., 0., z], k, l]...](images/ejercicio18m_7.gif)
![sistema := [[semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R], [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r], [muelle, [0., 0., 0.], [0., 0., z], k, l]...](images/ejercicio18m_8.gif)
Definimos las componentes de la Lagrangiana para después obtener las ecuaciones de Lagrange o del movimiento.
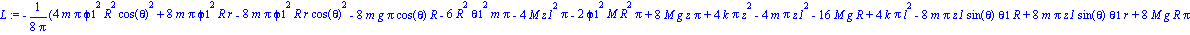
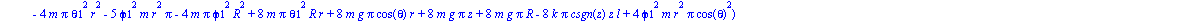
Ecuaciones del movimiento
| > |
ecua:=simplify(ec_lag()); |

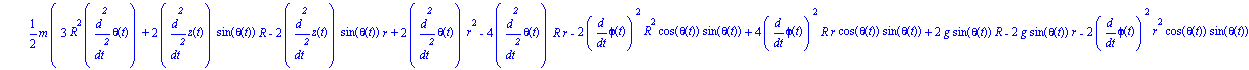

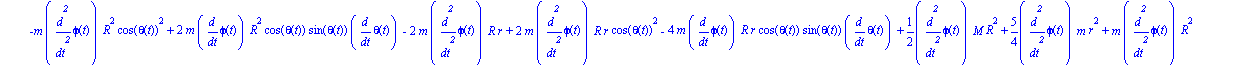

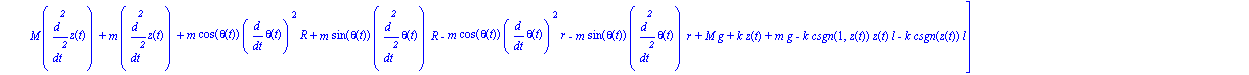
Damos valores a los parámetros que anteriormente habíamos definido por nombre, para obtener una representación del sistema, comprobar que el sistema se ha definido correctamente y poder realizar la integración numérica.
| > |
M:=2:R:=10:m:=1:l:=10:g:=9.8:k:=10:r:=2.5: |
| > |
fG([evalf(Pi/3),evalf(Pi/8),5.]); |
![[Plot]](images/ejercicio18m_17.gif)
Integración numérica, indicando valores iniciales y velocidades iniciales.
| > |
res:=fint([evalf(Pi/3),0.3,evalf(Pi/8),0.6,5.,0.1]); |

Animación del movimiento durante 5 segundos con 40 imágenes.
![[Plot]](images/ejercicio18m_19.gif)
A continuación representamos las gráficas de las coordenadas generalizadas en el tiempo, así como la relación entre las distintas coordenadas generalizadas a lo largo del tiempo.
| > |
odeplot(res,[t,theta(t)],t=0..5,color=red); |
![[Plot]](images/ejercicio18m_20.gif)
| > |
odeplot(res,[t,phi(t)],t=0..5,color=green); |
![[Plot]](images/ejercicio18m_21.gif)
| > |
odeplot(res,[t,z(t)],t=0..5,color=blue); |
![[Plot]](images/ejercicio18m_22.gif)
| > |
odeplot(res,[z(t),phi(t)],0..4); |
![[Plot]](images/ejercicio18m_23.gif)
| > |
odeplot(res,[theta(t),phi(t)],0..4); |
![[Plot]](images/ejercicio18m_24.gif)
| > |
odeplot(res,[z(t),theta(t)],0..4); |
![[Plot]](images/ejercicio18m_25.gif)
![]()
![]()
![]()
![]()
![sistema := [[semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R], [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r], [muelle, [0., 0., 0.], [0., 0., z], k, l]...](images/ejercicio18m_5.gif)
![]()
![]()
![sistema := [[semiaro, [0, 0, z+R-2*R/Pi], rotp, M, R], [disco, [-(R-r)*sin(theta)*sin(phi), (R-r)*sin(theta)*cos(phi), z+R-(R-r)*cos(theta)], rotdisco, m, r], [muelle, [0., 0., 0.], [0., 0., z], k, l]...](images/ejercicio18m_8.gif)
![]()
![]()

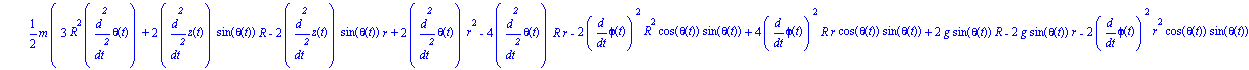

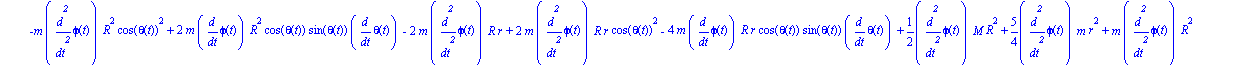

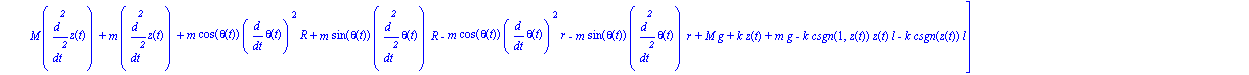
![[Plot]](images/ejercicio18m_17.gif)
![]()
![[Plot]](images/ejercicio18m_19.gif)
![[Plot]](images/ejercicio18m_20.gif)
![[Plot]](images/ejercicio18m_21.gif)
![[Plot]](images/ejercicio18m_22.gif)
![[Plot]](images/ejercicio18m_23.gif)
![[Plot]](images/ejercicio18m_24.gif)
![[Plot]](images/ejercicio18m_25.gif)