ENUNCIADO EJEMPLO 8

          Se considera un sistema compuesto por una mesa y un disco que se apoya sobre ella. Además, existe un árbol vertical que gira con velocidad w . El disco, de masa m y radio R, está ligado al árbol por un eje de longitud l y masa despreciable de tal manera que  pivota sin rozamiento en el punto O y puede deslizarse libremente por el eje vertical del árbol. El disco rueda y desliza sobre la mesa, se admite que no llega a levantarse sobre ella.

   Paso 0. Reiniciación de las variables del sistema y llamada a los paquetes linalg, plots y plottools.

>

restart:

>	with(linalg):with(plots):with(plottools):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name changecoords has been redefined

Warning, the name arrow has been redefined

>	libname:="C:/",libname:

>	with(mecapac3d):

   Paso 1. Definimos las coordenadas generalizadas del sistema en una lista que se denominará cg.

>	cg:=[omega,alpha,phi];

   Paso 2. Definición mediante variables de los elementos que forman el sistema mecánico.

>	xg:=[l*sin(alpha)*cos(omega),l*sin(alpha)*sin(omega),R*sin(alpha)];

>	rot1:=rota(phi,3):

>	rot2:=rota(-alpha,2):

>	rot3:=rota(omega,3):

>	rot:=evalm((rot3&*rot2)&*rot1):

>	d1:=[disco,xg,rot,m,R];

>

>	H:=l*cos(alpha)+R*sin(alpha):

>	s1:=[segmento,[0,0,H],[0,0,H+2],red];

>	s2:=[segmento,[0,0,H],xg,black];

>	d2:=[disco,[0,0,0],rota(0,1),m,3*R]:

   Paso 3. Definición de los elementos gráficos que definiran nuestro sistema de ejes.

>	ejeX:=[vector,[0,0,0],[14,0,0],red]:

>	ejeY:=[vector,[0,0,0],[0,14,0],green]:

>	ejeZ:=[vector,[0,0,0],[0,0,12],blue]:

>	TO := [texto,[0,0,-1],"O"]:

>	TX := [texto,[14,0,1],"Y"]:

>	TY := [texto,[0,14,1],"Y"]:

>	TZ := [texto,[0,0,13],"Z"]:

   Paso 4. Definición de la variable sistema que agrupa en una lista todos los elementos anteriores

>	sistema:=[d1,d2,s1,s2,ejeX,ejeY,ejeZ,TO,TX,TY,TZ]:

   Paso 5. Obtención de la energía cinética del sistema mediante fT asignándola a la variable T.

>	T:=fT(sistema);

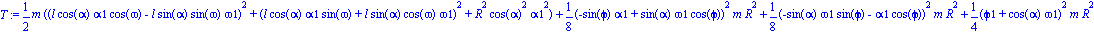
   Paso 6. Obtención de la energía potencial del sistema mediante fV asignándola a la variable V.

>	V:=fV(sistema);

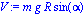
   Paso 7. Obtención de la lagrangiana como diferencia de energías entre la energía cinética y la potencial.

>

L:=T-V;

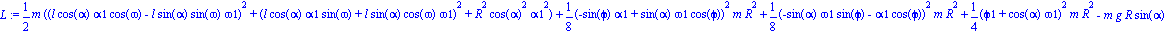
   Paso 8. Obtención de las ecuaciones de lagrange para las dos coordenadas generalizadas mediante el operador Ec_lag

>	ecua:=map(ec_lag(),cg):

   Paso 9. Asignación de valores numéricos a los parámetros que queden sun asignar para poder proceder a la integración numérica.

>	R:=3; l:=4; m:=1; g:=9.8;

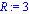
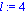
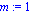
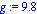
   Paso 10. Visualizamos las condiciones iniciales del problema.

>	fG([evalf(Pi/8),Pi/2,evalf(Pi)]);

   Paso 11. Integración numérica del problema mediante la función fint asignando el resultado a la variable res.

>	res:=fint([Pi/8,1,Pi/2,1,Pi,1]);

   Paso 12. Procedemos a realizar una animación del movimiento del conjunto por medio de la función dibu3.

>	dibu3(1,40);

   Paso 13. Representación gráfica de las evoluciones temporales de la evolución temporal de phi, omega y alpha mediante odeplot.

>	p1:=odeplot(res,[t,phi(t)],0..5,color=red):

>	p2:=odeplot(res,[t,omega(t)],0..5,color=blue):

>	p3:=odeplot(res,[t,alpha(t)],0..5,color=green):

>	display({p1,p2,p3});

>